
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
We now have many of the tools we need to write computer programs. We have the primitive operations for arithmetic computation, the primitive operations to manipulate words and sentences, and a way to choose between alternative computations. One thing that we still lack is a way to deal systematically with data aggregates--collections of data. We want to be able to say "carry out this computation for each member of that aggregate." Processing large amounts of data uniformly is one of the abilities that distinguish computers from mere pocket calculators.
InitialsTo make this concrete, we'll look at a very simple example. I'd like to write a procedure that can figure out a person's initials, like this:
? show initials [George Harrison] [G H]
One obvious approach is to find the initials of the first name and the last name:
to initials :name output sentence (first first :name) (first last :name) end
The trouble is that this approach doesn't work for people with middle
names. We'd like our initials procedure to be able to handle
any length name. But it doesn't:
? show initials [John Alec Entwistle] [J E] ? show initials [Peter Blair Denis Bernard Noone] [P N]
What we want is this:
? show initials.in.our.dreams [John Alec Entwistle] [J A E] ? show initials.in.our.dreams [Peter Blair Denis Bernard Noone] [P B D B N]
If we knew that the input would have exactly five names, we could extract the first letter of each of them explicitly. But you never know when some smart alec will ask you to
show initials [Princess Angelina Contessa Louisa Francesca ~
Banana Fana Bo Besca the Third]
If you've programmed before in other languages, then one solution will
immediately occur to you. You create a variable n whose value
is the number of words in the input, then you have a variable i
that takes on all possible values from 1 to n, and you select
the ith word from the input and pull out its first letter.
Most languages have a special notation for this sort of computation:
for i = 1 to n : ... : next i (BASIC)
for 1 := 1 to n do begin ... end (Pascal)
for (i=1; i<=n; i++) { ... } (C)
All of these have the same meaning: Carry out some instructions
(the part shown as ... above) repeatedly, first with the variable
named i having the value 1, then with i equal to 2,
and so on, up to i equal to n. This technique is called
numeric iteration. "Iteration" means repetition, and it's
"numeric" iteration because the repetition is controlled by a variable
that takes on a sequence of numeric values.
We can do the same thing in Logo, although, as we'll soon learn, it's not the usual approach that Logo programmers take to this problem.
to initials :name
local "result
make "result []
for [i 1 [count :name]] ~
[make "result sentence :result first (item :i :name)]
output :result
end
(The reason I declare result as local, but not i,
is that Logo's for automatically makes its index variable local
to the for itself. There is no variable i outside
of the for instruction.)
The command for takes two inputs. The second input is an
instruction list that will be carried out repeatedly. The first input
controls the repetition; it is a list of either three or four members: a
variable name, a starting value, a limit value, and an optional increment.
(The variable named by the first member of the list is called the index
variable. For example:
? for [number 4 7] [print :number] 4 5 6 7 ? for [value 4 11 3] [print :value] 4 7 10
In the first example, number takes on all integer values
between 4 and 7. In the second, value's starting value is 4,
and on each repetition its new value is 3 more than last time.
Value never actually has its limiting value of 11; the next
value after 10 would have been 13, but that's bigger than the limit.
For can count downward instead of upward:
? for [i 7 5] [print :i] 7 6 5 ? for [n 15 2 -6] [print :n] 15 9 3 ? for [x 15 2 6] [print :x] ?
The last example has no effect. Why? The increment of 6 implies that
this invocation of for should count upward, which means that the
for continues until the value of x is greater than
the limit, 2. But the starting value, 15, is already greater than
2.
If no increment is given in the first input to for, then
for will use either 1 or -1 as the
increment, whichever is compatible with the starting and limit values.
Although I've been using constant numbers as the starting value, limit
value, and increment in these examples, for can handle any Logo
expression, represented as a list, for each of these:
to spread :ends for [digit [first :ends] [last :ends]] [type :digit] print [] end ? spread 19 123456789 ? spread 83 876543
More formally, the effect of for is as follows. First it creates the
local index variable and assigns it the starting value. Then for
carries out three steps repeatedly: testing, action, and incrementing. The
testing step is to compare the current value of the index variable with the
limit value. If the index variable has passed the limit, then the for
is finished. ("Passed" means that the index variable is greater than the
limit, if the increment is positive, or that the index variable is less than
the limit, if the increment is negative.) The action step is to evaluate
the instructions in the second input to for. The incrementing step is
to assign a new value to the index variable by adding the increment to the
old value. Then comes another round of testing, action, and incrementing.
So, for example, if we give Logo the instruction
show initials [Raymond Douglas Davies]
then the for instruction within initials is equivalent
to this sequence of instructions:
local "i ; initialize index variable make "i 1 if (:i > 3) [stop] ; testing make "result (se :result first "Raymond) ; action (result is [R]) make "i :i+1 ; incrementing (i is 2) if (:i > 3) [stop] ; testing make "result (se :result first "Douglas) ; action (result is [R D]) make "i :i+1 ; incrementing (i is 3) if (:i > 3) [stop] ; testing make "result (se :result first "Davies) ; action (result is [R D D]) make "i :i+1 ; incrementing (i is 4) if (:i > 3) [stop] ; testing
except that the stop instruction in the testing step stops
only the for instruction, not the initials procedure.
Computers were originally built to deal with numbers. Numeric iteration matches closely the behind-the-scenes sequence of steps by which computers actually work. That's why just about every programming language supports this style of programming.
Nevertheless, a for instruction isn't anything like the way
you, a human being, would solve the initials problem without a
computer. First of all, you wouldn't begin by counting the number of words
in the name; you really don't have to know that. You'd just say, for
example, "First of Raymond is R; first of Douglas is D; first of Davies is
D." When you ran out of names, you'd stop.
The manipulation of the result variable to collect the results also
seems unnatural. You wouldn't think, "I'm going to start with an empty
result; then, whatever value result has, I'll throw in an R; then,
whatever value result now has, I'll throw in a D" and so on.
In fact, if you had to explain to someone else how to solve this problem, you probably wouldn't talk about a sequence of steps at all. Rather, you'd draw a picture like this one:
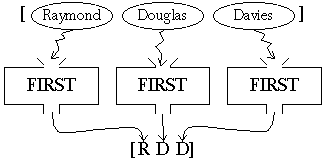
To explain the picture, you'd say something like "Just take the
first of each word." You wouldn't even mention the need to put the
results together into a sentence; you'd take that for granted.
In Logo we can write an initials procedure using the same way of
thinking that you'd use in English:
to initials :name output map "first :name end
The map procedure means "collect the results of
doing this for each of those."
As this example illustrates, map is easy to use. But it's a
little hard to talk about, because it's a function of a function. So first
we'll take a detour to talk more precisely about functions in general.
A function is a rule for turning one value (called the argument) into another. If you've studied algebra you'll remember numeric function rules such as
but not all functions are numeric, and not all rules need be expressed as algebraic formulas. For example, here is the Instrument function, which takes a Beatle as its argument and returns his instrument:
| argument | result |
|---|---|
| John | rhythm guitar |
| Paul | bass guitar |
| George | lead guitar |
| Ringo | drums |
This particular function has only four possible arguments. Other
functions, like f(x) above, may have infinitely many possible arguments.
The set of possible arguments is called the domain of the
function. Similarly, the set of possible result values is called the
range of the function.*
*It's a little awkward to talk about
the domain of a function that takes two arguments. That is, it's easy to
say that the domain of the function represented by the
first operation
is words or lists, but how do we describe item? We could loosely say
"its domain is numbers and words or lists," but that sounds as if either
argument could be any of those. The most precise way to say it is this:
"The domain of item is pairs of values, in which the first member of
the pair is a positive integer and the second member is a word or list of
length greater than or equal to the first member of the pair." But for
ordinary purposes we just rephrase the sentence to avoid the word "domain"
altogether: "Item takes two inputs; the first must be a positive
integer and the second must be a word or list..."
Functions can be represented in many ways. (We've seen two in this section: formulas and tables.) One way to represent a function is with a Logo operation. Here are Logo representations of the two functions we've discussed:
to f :x output 3*:x - 6 end to instrument :beatle if :beatle = "John [output [rhythm guitar]] if :beatle = "Paul [output [bass guitar]] if :beatle = "George [output [lead guitar]] if :beatle = "Ringo [output [drums]] end
(What if we give instrument an input that's not in the
domain of the function? In that case, it won't output any value, and a Logo
error message will result. Some people would argue that the procedure
should provide its own, more specific error message.)
I've been careful to say that the Logo operation represents the function, not that it is the function. In particular, two Logo procedures can compute the same function--the same relationship between input and output values--by different methods. For example, consider these Logo operations:
to f :x to g :x output 3*:x - 6 output 3 * (:x-2) end end
The Logo operations f and g carry out two different
computations, but they represent the same function. For example, to compute
f 10 we say 3×10=30, 30-6=24; to compute
g 10 we say 10-2=8, 3×8=24. Different computations,
but the same answer. Functional programming means, in part, focusing our
attention on the inputs and outputs of programs rather than on the sequence
of computational steps.
Just as a Logo operation represents a function, the procedure's inputs
similarly represent the arguments to the corresponding function.
For example, that instrument function I presented earlier has Beatles (that
is to say, people) as its domain and has musical instruments as its range.
But Logo doesn't have people or instruments as data types, and so the
procedure instrument takes as its input the name of a
Beatle (that is, a word) and returns as its output the name of an
instrument (a sentence). Instrument is a function from Beatles to
instruments, but instrument is an operation from words to
sentences.
We're about to see a similar situation when we explore map.
The map function--that is, the function that map
represents--is a function of functions. One of the arguments to
the map function is itself a function. The corresponding input to Logo's
map procedure should be a procedure. But it turns out that
Logo doesn't quite allow a procedure to be an input to another procedure;
instead, we must use the name of the procedure as the input, just as
we use the name of a Beatle as the input to instrument.
I know this sounds like lawyer talk, and we haven't written any programs for
a while. But here's why this is important: In order to understand the
purpose of map, you have to think about the map
function, whose domain is functions (and other stuff, as we'll see in a
moment). But in order to understand the notation that you use with
map in Logo, you have to think in terms of the Logo operation,
whose input is words (names of procedures). You have to be clear about this
representation business in order to be able to shift mentally between these
viewpoints.
Map
Map takes two inputs. The first is a word, which must be the name
of a one-input Logo operation. The second can be any datum. The output
from map is either a word or a list, whichever is the type of the
second input. The members of the output are the results of applying the
named operation to the members of the second input.
? show map "first [Rod Argent] [R A]
In this example, the output is a list of two members, just as the second
input is a list of two members. Each member of the output is the result of
applying first to one of the members of map's
second input.
Many people, when they first meet map, are confused by the
quoting of its first input. After all, I made a fuss back in Chapter
2 about the difference between these two examples:
? print Hello I don't know how to Hello ? print "Hello Hello
You learned that a quoted word means the word itself, while an unquoted word
asks Logo to invoke a procedure. But now, when I want to use the
first procedure as input to map, I'm quoting its
name. Why?
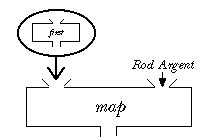
All that effort about the domains of functions should help you understand the notation used here. Start by ignoring the Logo notation and think about the domain of the map function. We want the map function to have another function, the function "first" in this case, as one of its arguments:
It's tempting to say that in Logo, a function is represented by a procedure,
so map represents map, and first represents first.
If this were algebra notation, I'd say map(first, Rod Argent),
so in Logo I'll say
show map first [Rod Argent] ;; wrong!
But when a Logo instruction has two unquoted procedure names in a row, that
doesn't mean that the second function is used as argument to the first!
Instead, it means that the output from invoking the second function
is used as the argument to the first. In this case, we'd be
composing map and first:
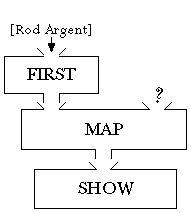
As the plumbing diagram shows, the list that we intended as the second input
to map actually ends up as the input to first, and
Logo will complain because map isn't given enough inputs.
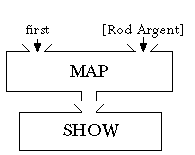
Instead, as I said earlier, we must use the name of the
first procedure to represent it. That gives this diagram:
Here's another simple example. Logo has a primitive operation
uppercase that takes a word as input, and outputs the same word
but in all capital letters:
? print uppercase "young YOUNG
What if we want to translate an entire sentence to capital letters? The
uppercase primitive doesn't accept a sentence as its input:
? show uppercase [neil young] uppercase doesn't like [neil young] as input.
But we can use map to translate each word separately and
combine the results:
? show map "uppercase [neil young] [NEIL YOUNG]
Ordinarily map works with one-argument functions. But we can
give map extra arguments (by enclosing the invocation of
map in parentheses, as usual) so that it can work with
functions of more than one argument.
? show (map "item [2 1 2 3] [john paul george ringo]) [o p e n] ? show (map "sum [1 2 3] [40 50 60] [700 800 900]) [741 852 963]
Each input after the first provides values for one input to the mapped
function. For example, [2 1 2 3] provides four values for the
first input to item. The input lists must all have the same
length (two lists of length four in the item example, three
lists of length three in the sum example).
In the examples so far, the input data have been lists. Here's an example
in which we use map with words. Let's say we're writing a
program to play Hangman, the word game in which one player guesses letters
in a secret word chosen by the other player. At first the guesser sees only
a row of dashes indicating the number of letters in the word; for each
guess, more letters are revealed. We aren't going to write the entire
program yet, but we're ready to write the operation that takes the secret
word, and a list of the letters that have been guessed so far, and outputs a
row of letters and dashes as appropriate.
to hangword :secret :guessed output map "hangletter :secret end to hangletter :letter output ifelse memberp :letter :guessed [:letter] ["_] end ? print hangword "potsticker [e t a o i n] _ot_ti__er ? print hangword "gelato [e t a o i n] _e_ato
Notice that hangletter depends on Logo's dynamic scope to have
access to hangword's local variable named guessed.
» Write an operation exaggerate that takes a sentence as
input and outputs an exaggerated version:
? print exaggerate [I ate 3 potstickers] I ate 6 potstickers ? print exaggerate [The chow fun is good here] The chow fun is great here
It should double all the numbers in the sentence, and replace "good" with "great," "bad" with "terrible," and so on.
A function whose domain or range includes functions is called a
higher order function. The function represented by
map is a higher order function. (We may speak loosely and say
that map is a higher order function, as long as you remember
that Logo procedures aren't really functions!) It's tempting to say that the
map procedure itself is a "higher order procedure," but in
Logo that isn't true. Procedures aren't data in Logo; the only data types
are words and lists. That's why the input to map is a word,
the name of a procedure, and not the procedure itself. Some languages do
treat procedures themselves as data. In particular, the language Scheme is
a close relative of Logo that can handle procedures as data. If this way of
thinking appeals to you, consider learning Scheme next!
Filter
The purpose of map is to transform each member of an
aggregate (a list or a word) by applying some function to it. Another
higher order function, filter, is used to select some
members of an aggregate, but not others, based on a criterion expressed as a
predicate function. For example:
? show filter "numberp [76 trombones, 4 calling birds, and 8 days] [76 4 8] to vowelp :letter output memberp :letter "aeiou end ? show filter "vowelp "spaghetti aei to beatlep :person output memberp :person [John Paul George Ringo] end ? show filter "beatlep [Bob George Jeff Roy Tom] [George]
What happens if we use the initials procedure that we wrote with
people's names in mind for other kinds of names, such as organizations or
book titles? Some of them work well:
? show initials [Computer Science Logo Style] [C S L S] ? show initials [American Civil Liberties Union] [A C L U]
but others don't give quite the results we'd like:
? show initials [Association for Computing Machinery] [A f C M] ? show initials [People's Republic of China] [P R o C]
We'd like to eliminate words like "for" and "of" before taking the first
letters of the remaining words. This is a job for filter:
to importantp :word output not memberp :word [the an a of for by with in to and or] end to initials :name output map "first (filter "importantp :name) end ? show initials [Association for Computing Machinery] [A C M] ? show initials [People's Republic of China] [P R C]
ReduceOf course, what we'd really like is to have those initials in the form of a single word: ACLU, CSLS, ACM, and so on. For this purpose we need yet another higher order function, one that invokes a combining function to join the members of an aggregate.
? show reduce "word [C S L S] CSLS ? show reduce "sum [3 4 5 6] 18 ? show reduce "sentence "UNICEF [U N I C E F]
Reduce takes two inputs. The first must be the name of a
two-input operation; the second can be any nonempty word or list.
to acronym :name output reduce "word initials :name end
In practice, the first input to reduce won't be any old
operation; it'll be a constructor. It'll be something that doesn't
care about the grouping of operands; for example, sum is a good
choice but difference is problematic because we don't know
whether
reduce "difference [5 6 7]
means 5-(6-7) or (5-6)-7, and the grouping affects the answer. Almost
all the time, the constructor will be word,
sentence, sum, or product. But
here's an example of another one:
to bigger :a :b output ifelse :a > :b [:a] [:b] end to biggest :nums output reduce "bigger :nums end ? show biggest [5 7 781 42 8] 781
So far you've seen three higher order functions: map,
filter, and reduce. How do you decide which one to
use for a particular problem?
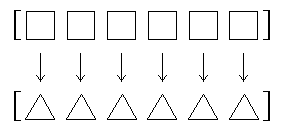
Map transforms each member of a word or list individually. The
result contains as many members as the input.
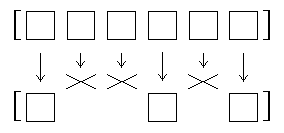
Filter selects certain members of a word or list and discards the
others. The members of the result are members of the input, without
transformation, but the result may be smaller than the original.
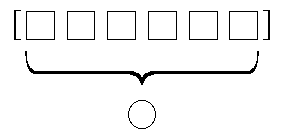
Reduce transforms the entire word or list into a single result
by combining all of the members in some way.
In several of the examples in this chapter, I've had to write "helper"
procedures such as hangletter, importantp, and
bigger that will never be used independently, but are needed
only to provide the function argument to a higher order function. It would
be simpler if we could avoid writing these as separate procedures.
Does that sound confusing? This is one of those ideas for which an example is worth 1000 words:
to hangword :secret :guessed output map [ifelse memberp ? :guessed [?] ["_]] :secret end
Until now, the first input to map has always been a word,
used to represent the function with that word as its name. In this example
we see how a nameless function can be represented: as a list containing a
Logo expression, but with question marks where the function's argument
belongs. Such a list is called a template.
? show filter [memberp ? [John Paul George Ringo]] ~
[Bob George Jeff Roy Tom]
[George]
Anonymous functions of more than one argument are a little uglier. Instead
of ? for the argument, you must use ?1 for the
first, ?2 for the second, and so on.
to biggest :nums output reduce [ifelse ?1 > ?2 [?1] [?2]] :nums end
Notice that the templates don't say output, as the named
procedures did. That's because procedures are made of
instructions, whereas these are expression templates.
When input values are "plugged in" for the question marks, the template
becomes a Logo expression, which means that when evaluated it has a value.
If the template said output, it would be saying to use that
value as the output from the procedure containing it! (I'm just
repeating the point made earlier that output immediately stops
the procedure it's in, even if there are more instructions below it.)
Map combines the partial results into a list, if the second
argument is a list, or into a word, if it's a word. Sometimes this behavior
isn't quite what you want. An alternative is map.se (map to
sentence), which makes a sentence of the results. Here are some examples.
? make "numbers [zero one two three four five six seven eight nine] ? show map [item ?+1 :numbers] 5789 fiveseveneightnine ? show map.se [item ?+1 :numbers] 5789 [five seven eight nine] ? show map [sentence (word "With ?) "You] [in out] [[Within You] [Without You]] ? show map.se [sentence (word "With ?) "You] [in out] [Within You Without You] ? show map.se [sentence ? "Warner] [Yakko Wakko Dot] [Yakko Warner Wakko Warner Dot Warner] ? show map [sentence ? "Warner] [Yakko Wakko Dot] [[Yakko Warner] [Wakko Warner] [Dot Warner]]
As these examples show, sometimes map does what you want, but
sometimes map.se does, depending on the "shape" you want your
result to have. Do you want a word, a sentence, or a structured list?
Suppose we have two sets of things, and we want all the pairings of one of these with one of those. An example will make clear what's desired:
? show crossproduct [red blue green] [shirt pants] [[red shirt] [blue shirt] [green shirt] [red pants] [blue pants] [green pants]]
This is a tricky example because there are two different mistakes we could make. We don't want to "flatten" the result into a sentence:
[red shirt blue shirt green shirt red pants blue pants green pants]
but we also don't want all the shirts in one list and all the pants in another:
[[[red shirt] [blue shirt] [green shirt]] [[red pants] [blue pants] [green pants]]]
Here's the solution:
to crossproduct :these :those output map.se [prepend.each :these ?] :those end to prepend.each :these :that output map [sentence ? :that] :these end
» Notice that this solution uses both map and
map.se. Try to predict what would happen if you used
map both times, or map.se both times, or
interchanged the two. Then try it on the computer and be sure you
understand what happens and why!
By the way, this is a case in which we still need a named helper function
despite the use of templates, because otherwise we'd have one template
inside the other, and Logo couldn't figure out which ? to
replace with what:
to crossproduct :these :those output map.se [map [sentence ? ?] :these] :those ; (wrong!) end
Just as map.se is a variant of map,
find is a variant of filter, for the situations in
which you only want to find one member that meets the criterion,
rather than all the members. (Perhaps you know in advance that there will
only be one, or perhaps if there are more than one, you don't care which you
get.)
to spellout :card
output (sentence (butlast :card) "of
(find [equalp last :card first ?]
[hearts spades diamonds clubs]))
end
? print spellout "5d
5 of diamonds
? print spellout "10h
10 of hearts
Sometimes what you want isn't a function at all. You want to take some
action for each member of an aggregate. The most common one is to
print each member on a separate line, in situations where you've computed a
long list of things. You can use foreach with an
instruction template, rather than an expression template as used
with the others. The template is the last argument, rather than the first,
to follow the way in which the phrase "for each" is used in English: For
each of these things, do that.
? foreach (crossproduct [[ultra chocolate] pumpkin [root beer swirl]
ginger] [cone cup]) "print
ultra chocolate cone
pumpkin cone
root beer swirl cone
ginger cone
ultra chocolate cup
pumpkin cup
root beer swirl cup
ginger cup
If you look closely at the letters on your computer screen you'll see that they are made up of little dots. One simple pattern represents each letter in a rectangle of dots five wide and seven high, like this:
* ***** ***** **** ***** * * * * * * * * * * * * * * * * ***** **** * * * *** * * * * * * * * * * * * * * * * * * ***** ***** **** *****
The following program allows you to spell words on the screen in big letters like these. Each letter's shape is kept as the value of a global variable with the letter as its name. (I haven't actually listed all 26 letters.) The value is a list of seven words, each of which contains five characters, some combination of spaces and asterisks.
to say :word for [row 1 7] [foreach :word [sayrow :row ?] print []] print [] end to sayrow :row :letter type item :row thing :letter type "| | end make "b [|*****| |* *| |* *| |**** | |* *| |* *| |*****|] make "r [|*****| |* *| |* *| |*****| |* * | |* * | |* *|] make "i [|*****| | * | | * | | * | | * | | * | |*****|] make "a [| * | | * * | |* *| |*****| |* *| |* *| |* *|] make "n [|* *| |** *| |** *| |* * *| |* **| |* **| |* *|] ? say "brian ***** ***** ***** * * * * * * * * * * ** * * * * * * * * ** * **** ***** * ***** * * * * * * * * * * * ** * * * * * * * * ** ***** * * ***** * * * *
» Modify the program so that say takes another input, a
number representing the size in which you want to print the letters. If the
number is 1, then the program should work as before. If the number is 2,
each dot should be printed as a two-by-two square of spaces or asterisks; if
the number is 3, a three-by-three square, and so on.
CascadeFinally, sometimes you want to compose a function with itself several times:
? print first bf bf bf bf [The Continuing Story of Bungalow Bill] Bungalow ? print first (cascade 4 "bf [The Continuing Story of Bungalow Bill]) Bungalow
Cascade takes three inputs. The first is a number,
indicating how many times to invoke the function represented by the second
argument. The third argument is the starting value.
to power :base :exponent output cascade :exponent [? * :base] 1 end ? print power 2 8 256 to range :from :to output cascade :to-:from [sentence ? (1+last ?)] (sentence :from) end ? show range 3 8 [3 4 5 6 7 8]
Like map, cascade can be used with extra inputs to
deal with more than one thing at a time. One example in which multi-input
cascade is useful is the Fibonacci sequence. Each number in
the sequence is the sum of the two previous numbers; the first two numbers
are 1. So the sequence starts
A formal definition of the sequence looks like this:
| F0 = 1 |
| F1 = 1 |
| Fn = Fn-1 + Fn-2, n>1 |
In order to compute, say, F23, we must know both F22 and F21. As we work our way up, we must always remember the two most recent values, like this:
| Most recent value | Next most recent value | |
|---|---|---|
| start | 1 | 0 |
| step 1 | 1 | 1 |
| step 2 | 2 | 1 |
| step 3 | 3 | 2 |
| step 4 | 5 | 3 |
| ... | ... | ... |
| step 22 | F22 | F21 |
| step 23 | F22+F21 | F22 |
To express this using cascade, we can use ?1 to
mean the most recent value and ?2 to mean the next most
recent. Then at each step, we need a function to compute the new
?1 by adding the two known values, and a function to copy the
old ?1 as the new ?2:
to fib :n output (cascade :n [?1+?2] 1 [?1] 0) end ? print fib 5 8 ? print fib 23 46368
Another situation in which multi-input cascade can be useful is
to process every member of a list, using ?1 to remember the
already-processed ones and ?2 to remember the still-waiting
ones. The simplest example is reversing the words in a sentence:
to reverse :sent
output (cascade (count :sent)
[sentence (first ?2) ?1] []
[butfirst ?2] :sent)
end
? print reverse [how now brown cow]
cow brown now how
?1 |
?2 |
|
|---|---|---|
| start | [] |
[how now brown cow] |
| step 1 | [how] |
[now brown cow] |
| step 2 | [now how] |
[brown cow] |
| step 3 | [brown now how] |
[cow] |
| step 4 | [cow brown now how] |
[] |
Here is the general notation for multi-input cascade:
(cascade howmany function1 start1 function2 start2 ...)
There must be as many function inputs as
start inputs. Suppose there are n pairs of inputs;
then each of the functions must accept n inputs. The
starts provide the initial values for ?1,
?2, and so on; each function provides the next value for one of
those. Cascade returns the final value of ?1.
It's time to put these programming tools to work in a more substantial project. You're ready to write a computer program that plays a family of games like MastermindTM. The computer picks a secret list of colors; the human player makes guesses. (The number of possible colors can be changed to tune the difficulty of the game.) At each turn, the program should tell the player how many colors in the guess are in the correct positions in the secret list and also how many are in the list, but not at the same positions. For example, suppose the program's secret colors are
red green blue violetand the player guesses
red orange yellow green
There is one correct-position match (red, because it's the first color in both lists) and one incorrect-position match (green, because it's second in the computer's list but fourth in the player's list).
In the program, to reduce the amount of typing needed to play the game,
represent each color as a single letter and each list of colors as a word.
In the example above, the computer's secret list is represented as
rgbv and the player's guess as royg.
There are two possible variations in the rules, depending on whether or not
color lists with duplications (such as rgrb, in which red
appears twice) are allowed. The program will accept a true-or-false input
to determine whether or not duplicates are allowed.
Here's an example of what an interaction with the program should look like:
? master "roygbiv 4 "false What's your guess? royg You have 1 correct-position matches and 2 incorrect-position matches. What's your guess? rogy You have 1 correct-position matches and 2 incorrect-position matches. What's your guess? orygbv You must guess exactly 4 colors. What's your guess? oryx The available colors are: roygbiv What's your guess? oryr No fair guessing the same color twice! What's your guess? oryg You have 0 correct-position matches and 3 incorrect-position matches. What's your guess? rbyg You have 1 correct-position matches and 2 incorrect-position matches. What's your guess? boyg You have 0 correct-position matches and 3 incorrect-position matches. What's your guess? roby You have 1 correct-position matches and 3 incorrect-position matches. What's your guess? rybo You have 2 correct-position matches and 2 incorrect-position matches. What's your guess? ryob You win in 8 guesses! ?
If you prefer, just jump in and start writing the program. But I have a
particular design in mind, and you may find it easier to follow my plan.
The core of my program is written sequentially, in the form of a
for instruction that carries out a sequence of steps once for
each guess the user makes. But most of the "smarts" of the program are in
a collection of subprocedures that use functional programming style. That
is, these procedures are operations, not commands; they merely compute and
output a value without taking any actions. Pay attention to how these two
styles fit together. In writing the operations, don't use make
or print; each operation will consist of a single
output instruction.
» The first task is for the computer to make a random selection from the
available colors. Write two versions: choose.dup that allows
the same color to be chosen more than once, and choose.nodup
that does not allow duplication. Each of these operations should take two
inputs: a number, indicating how many colors to choose, and a word of all
the available colors. For example, to choose four colors from the rainbow
without duplication, you'd say
? print choose.nodup 4 "roygbiv briy
You'll find the Logo primitive pick helpful. It takes a
word or list as its input, and returns a randomly chosen member:
? print pick [Pete John Roger Keith] John ? print pick [Pete John Roger Keith] Keith ? print pick "roygbiv b
Writing choose.dup is a straightforward combination of
pick and cascade.
Choose.nodup is a little harder. Since we want to eliminate
any color we choose from further consideration, it's plausible to use a
multi-input cascade sort of like this:
(cascade :number-wanted
[add one color] "
[remove that color] :colors)
If we always wanted to choose the first available color, this would be just
like the reverse example earlier. But we want to choose a
color randomly each time. One solution is to rotate the available
colors by some random amount, then choose what is now the first color. To
use that idea you'll need a rotate operation that rotates a
word some random number of times, like this:
? rotate "roygbiv ygbivro ? rotate "roygbiv vroygbi ? rotate "roygbiv bivroyg
You can write rotate using cascade along with the
Logo primitive operation random. Random takes a
positive integer as its input, and outputs a nonnegative integer less than
its input. For example, random 3 will output 0,
1, or 2.
» The second task is to evaluate the player's guess. You'll need an
operation called exact that takes two words as inputs (you may
assume they are the same length) and outputs the number of correct-position
matches, and another operation called inexact that computes the
number of wrong-position matches. (You may find it easier to write a helper
procedure anymatch that takes two words as inputs, but outputs
the total number of matches, regardless of position.) Be sure to write
these so that they work even with the duplicates-allowed rule in effect.
For example, if the secret word is rgrb and the user guesses
yrrr, then you must report one exact and one inexact match, not
one exact and two inexact.
? print exact "rgrb "yrrr 1 ? print inexact "rgrb "yrrr 1 ? print inexact "royg "rgbo 2
Exact is a straightforward application of multi-input
map, since you want to look at each letter of the secret word
along with the same-position letter of the user's guess. My solution to
anymatch was to use map to consider each of the
available colors. For each color, the number of matches is the smaller of
the number of times it appears in the secret word and the number of times it
appears in the guess. (You'll need a helper procedure howmany
that takes two inputs, a letter and a word, and outputs the number of times
that letter occurs in that word.)
» Up to this point, we've assumed that the player is making legitimate
guesses. A valid guess has the right number of colors, chosen from the set
of available colors, and (perhaps, depending on the chosen rules) with no
color duplicated. Write a predicate valid.guessp that takes a
guess as its input and returns true if the guess is valid,
false otherwise. In this procedure, for the first time in this
project, it's a good idea to violate functional programming style by
printing an appropriate error message when the output will be
false.
» We now have all the tools needed to write the top-level game procedure
master. This procedure will take three inputs: a word of the
available colors, the number of colors in the secret word, and a
true or false to indicate whether or not duplicate
colors are allowed. After using either choose.dup or
choose.nodup to pick the secret word, I used a for
loop to carry out the necessary instructions for each guess.
Brian Harvey,
bh@cs.berkeley.edu