| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |
|
|
Program file for this chapter: pascal
This chapter and the next are about two related things: why different programming languages are different and how a programming language is implemented. To make the discussion concrete, I've chosen a specific language as an example: Pascal. That choice seems appropriate partly because Pascal is very different from Logo and partly because it is widely used as a vehicle for teaching introductory computer science, the same task I'm attempting in this book using Logo.*
*The recent trend in computer
science education has been a shift from Pascal to C or C++. I haven't
followed that trend in this book because from my perspective C illuminates
no new issues, it has a more complicated syntax, and it leaves out one
interesting Pascal feature: nested procedure definitions (block structure).
C++ does introduce the issue of object-oriented programming, but, I think,
not in a way that clarifies the issues; if you want to understand OOP you'd
do better to learn Object Logo.
For the purposes of this book I've written a program that translates a small subset of Pascal into a simulated machine language. You can get a real Pascal compiler for your computer that accepts the full language, and that's what you should do if you want to learn how to program in Pascal. I had two reasons for writing this subset compiler. One is that some readers may not otherwise have access to a Pascal compiler, and mine, despite its limitations, will enable you to explore the parts of the language I'm going to be talking about. The other is that the next chapter is about how a compiler works, and this compiler is accessible to examination because it's written in Logo.
When you're comparing two programming languages an obvious question to ask is "which is better?" Please don't use my partial Pascal compiler as the basis for an answer to that question; it wouldn't be fair. You already know my opinion, but my purpose in this chapter is not to convince you of it. Instead I want you to understand why each language is designed the way it is. For each of the language differences we'll examine, there are good reasons for either choice; the reasons that influence a language designer will depend on the overall goals he or she has for this language.
Perhaps the most important aspect of the design of a programming language is the programming paradigm that it encourages. A paradigm (it's pronounced "para" as in "parakeet" followed by "dime" as in ten cents) is an approach to organizing a complex program: How do you combine the primitives of a language to accomplish harder tasks? It's an aspect of programming style, but when people say "style" they're usually thinking of smaller details, such as the use of comments in procedure definitions or choosing sensible variable names. Perhaps an example of different paradigms will help.
Here's how the factorial function is usually computed in Logo, using a recursive operation:
to fact :n if :n=0 [output 1] output :n * fact :n-1 end
The goal is to multiply several numbers together, the integers
from 1 to :n. We do this by carrying out one multiplication in each
recursive invocation. This procedure is written in the
functional programming paradigm; the main tool for building
up complexity is composition of functions. In this example, the
result of the recursive fact invocation is composed with the primitive
* (multiplication) function.
Now consider this alternate approach:
to fact.seq :n localmake "product 1 for [i 1 :n] [make "product (:product * :i)] output :product end
This is an example of the sequential programming paradigm,
so called because the for instruction carries out a sequence of steps:
| • | Multiply the accumulated product by 1. | |
|---|---|---|
| • | Multiply the product by 2. | |
| • | Multiply it by 3. |
... and so on. Instead of a composition of functions, we have
a partial result stored in a box, the variable product. At each
step, the old value is replaced with an updated value.
Although fact.seq can be written in Logo, it's not the most natural
Logo style. Most versions of Logo don't even provide for as a
primitive command, although (as we saw in Volume 2) it can be written in
Logo.* As we've seen, Logo encourages the
functional programming paradigm, in which complicated
computations are achieved by means of function composition and recursion.
Logo encourages functional programming partly through
its emphasis on recursion rather than on iterative control structures,
and partly because lists are used as the main data aggregation mechanism.
As we saw in Chapter 3, lists encourage an aggregate to be built up one
member at a time (as recursive functions do), and discourage mutation
(which is crucial to the sequential approach).
*Even in Berkeley Logo,
for is a library procedure rather
than a true primitive.
In Pascal, the opposite is true. It's possible to write a recursive factorial function in Pascal:
function fact(n:integer): integer;
begin
if n=0 then
fact := 1
else
fact := n * fact(n-1)
end;
but a habitual Pascal programmer would be much more likely to write this function in sequential style:
function fact(n:integer): integer;
var product, i: integer;
begin
product := 1;
for i := 1 to n do
product := product * i;
fact := product
end;
(Don't worry, I know the details of the notation are a mystery to
you, but you should still be able to see the relationship between each Pascal
version and the corresponding Logo version. The only crucial point about
notation right now is that := is the Pascal assignment operator, like
make in Logo. We'll go into the details of Pascal syntax later.)
Here's a more complicated example, showing how data aggregates are used in the two paradigms. In Chapter 2 we explored the Simplex lock problem by computing the function
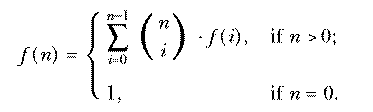
using these procedures:
to simplex :buttons output 2 * f :buttons end to f :n if equalp :n 0 [output 1] output cascade :n [? + ((choose :n (#-1)) * f (#-1))] 0 end
Here, the mathematical definition of f in terms of itself is
reflected in the recursive nature of the operation f. In Chapter 3, we
improved the efficiency of the procedure by remembering smaller values of
f to avoid recomputing them; similarly, instead of computing the
choose function separately each time, we used old values to compute
new ones:
to simplex :buttons
output 2 * first (cascade :buttons
[fput (sumprods butfirst ?2 ?1) ?1] [1]
[fput 1 nextrow ?2] [1 1])
end
to sumprods :a :b
output reduce "sum (map "product :a :b)
end
to nextrow :combs
if emptyp butfirst :combs [output :combs]
output fput (sum first :combs first butfirst :combs) ~
nextrow butfirst :combs
end
The recursive nature of f is less obvious in the second
implementation, but the overall technique is still composition of
functions. (Recall that the job of cascade is to invoke a
function repeatedly, in the pattern f(f(f(··· f(x)))). In this
case, cascade is computing two functions in parallel; one is a list of
values of the Simplex function f and the other is a row of Pascal's
triangle.) The availability of higher order functions (in this program
I've used cascade, map, and reduce) is another way
in which Logo encourages the functional paradigm.
In sequential style, the composition of functions is replaced by a sequence of steps in which values are stored in boxes (members of arrays) and repeatedly replaced with different values:
to simplex.seq :buttons
localmake "f (array :buttons+1 0)
localmake "combs (array :buttons+1 0)
local [left right]
setitem 0 :f 1
setitem 0 :combs 1
for [i 1 :buttons] [
setitem :i :f 0
make "right 0
for [j 0 :i-1] [
make "left :right
make "right item :j :combs
setitem :j :combs :left+:right
setitem :i :f (item :i :f) + (item :j :f)*(item :j :combs)
]
setitem :i :combs 1
]
output 2 * item :buttons :f
end
It may take some effort to convince yourself that this procedure
really computes the same results as the other versions! Within the
procedure, the array f contains the values f(0), f(1), ... as
they are computed one by one; the array combs contains one row (at a
time) of Pascal's triangle.
The procedure first puts f(0) into the zeroth position of the f array
and the first row of Pascal's triangle (containing just one 1) in the
combs array. Then comes a for loop that computes f(1), then f(2),
and so on, until the desired value is reached. An inner for loop
fills the same purpose as the sumprods function in the previous
version of simplex: It computes the sum of several terms, not by
function composition but by adding each term into the sum separately.
The instruction
setitem :i :f (item :i :f) + (item :j :f)*(item :j :combs)
adds one additional term to the sum each time it's carried out.
The sequential Simplex calculation looks bizarre in Logo, but it's much more natural in Pascal:
function simplex(buttons:integer): integer;
var left, right, i, j: integer;
f, combs: array [0..30] of integer;
begin
f[0] := 1;
combs[0] := 1;
for i := 1 to buttons do
begin
f[i] := 0;
right := 0;
for j := 0 to i-1 do
begin
left := right;
right := combs[j];
combs[j] := left+right;
f[i] := f[i] + (f[j] * combs[j])
end;
combs[i] := 1
end;
simplex := 2 * f[buttons]
end;
Pascal is well suited to this style of programming for several
reasons. One is that the f[i] notation for a member of an array is
more compact and more readable than Logo's use of procedure invocations
(calling item to examine an array member and setitem to modify
its value). Another, already mentioned, is that for is built into
Pascal. Perhaps most important is Pascal's block structure:
the keywords begin and end can be used to group what would
otherwise be separate instructions into one larger instruction. In Logo,
the instructions that are repeated in a for loop must be part of a
list, one of the inputs to the for procedure; in principle, the entire
for invocation is one Logo instruction line.
Both Logo and Pascal are compromises between the functional paradigm and
the sequential paradigm. (In Logo, turtle graphics programs are most often
done sequentially, whereas the manipulation of words and sentences is
generally done functionally.) But Logo is much more of a functional
language than Pascal, partly because it supports list processing (you can
create lists in Pascal, but it's painful), and even more importantly because
in Logo it's easy to invent higher order functions such as map and
cascade. Pascal programmers can't readily invent their own control
structures because there's nothing like run or apply in Pascal,
and the built-in control structures are all sequential ones. (In addition
to for, Pascal has equivalents to the while and do.until
commands in the Berkeley Logo library.) As another example, Logo's
ifelse primitive can be used either as a command or as an operation, but
the Pascal equivalent works only as a command.
Not all programming languages compromise between paradigms. It's rare these
days to see a purely sequential language, but it used to be common; both the
original Fortran language and the early microcomputer versions of BASIC
lacked the ability to handle recursive procedures. Purely functional
languages are not widely used in industry, but are of interest to many
computer science researchers; the best known example is called ML. In a
purely functional language, there is no assignment operator (like make
in Logo) and no mutators (like setitem or .setfirst).
There are other programming paradigms besides sequential and functional, although those are the oldest. The sequential paradigm came first because the actual digital computer hardware works sequentially; Fortran, which was the first higher level programming language, was initially viewed as merely an abbreviation for the computer's hardware instruction sequences.* The functional paradigm was introduced with Lisp, the second-oldest programming language still in use. Although Lisp is not a pure functional language (it does have assignment and mutation), its design is firmly based on the idea of functions as the way to express a computation.
*Today, we think of programming languages primarily as ways
to express problems, rather than as ways to model how computer hardware
works. This shift in attitude has allowed the development of non-sequential
paradigms. We design languages that are well matched to the problems we want
to solve, rather than well matched to the hardware we're using.
Another paradigm that's very popular today is object-oriented programming. In this paradigm, we imagine that instead of having a single computer carrying out a single program, the computational world includes many independent "objects," each of which can carry out programs on its own. Each object includes methods, which are like local procedures, and variables, just like the variables we've used all along except that each belongs to a particular object. If one object wants to know the value of another object's variable, the first object must send a message to the second. A message is a request to carry out a method, so the messages that each object accepts depends on the methods that it knows.
Logo has had a sort of glimmer of the object paradigm for many years, because many dialects of Logo include multiple turtles. To move a turtle, you send it a message, using a notation something like
ask 7 [forward 100]
to send a message to turtle number 7. But this notation, even
though it conveys some of the flavor of object-oriented programming, is not
truly representative of the paradigm. In a real object system, it would
be possible for specific turtles to have their own, specialized forward
methods. Turtle 7, for example, might be a special "dotted turtle" that
draws dotted lines instead of solid lines when it moves forward. One Logo
dialect, called Object Logo, does provide a genuine object capability.
Object-oriented programming fits naturally with the sort of problem in which the computer is modeling or simulating a bunch of real-world objects; in fact, the paradigm was invented for simulation programs, used to try to answer questions such as "Will it eliminate the traffic jams if we add another lane to this highway, or should we spend the money on more frequent bus service instead?" The objects in the simulation program are people, cars, buses, and lanes. Another example of a problem that lends itself to the object paradigm is a window system, such as the one in Mac OS or in Microsoft Windows. Each window is an object; when a window is displayed so as to hide part of another window, the new window must send a message to the hidden one telling it not to display the hidden region.
Some people argue that object-oriented programming should be used for every programming problem, not because the independent object metaphor is always appropriate but because using objects helps with information hiding; if every variable belongs to a specific object, the program is less likely to have the kind of bug in which one part of a program messes up a data structure that's used in another part. This can be particularly important, they say, in a large programming problem in which several programmers work on different pieces of the program. When the different programmers' procedures are put together, conflicts can arise, but the object paradigm helps isolate each programmer's work from the others. Although this argument has some merit, I'm cautious about any claim that one particular paradigm is best for all problems. I think programmers should be familiar with all of the major paradigms and be able to pick one according to the needs of each task.
Another important programming paradigm is called logic programming or declarative programming. In this approach, the programmer doesn't provide an algorithm at all, but instead lists known facts about the problem and poses questions. It's up to the language implementation to search out all the possible solutions to a question. We saw a very simplified version of this paradigm in the discussion of logic problems in Chapter 2. Logic programming is especially well suited to database problems, in which we pose questions such as "Who are all the employees of this company who work in the data processing division and have a salary above 40,000?" But, like all the paradigms I've mentioned, logic programming is universal; any problem that can be solved by a computer at all can be expressed as a logic program. Logic programming is quite popular in Japan and in Europe, but not so much in the United States, perhaps just because it wasn't invented here.
You use Logo by interacting with the language processor. You issue an instruction, Logo does what you've told it and perhaps prints a result, and then you issue another instruction. You can preserve a sequence of instructions by defining a procedure, in which case that procedure can be invoked in later instructions. But you don't have to define procedures; young children generally start using Logo by issuing primitive turtle motion commands one at a time. Defining procedures can be thought of as extending the repertoire of things Logo knows how to do for future interaction.
By contrast, you write a Pascal program as a complete entity, "feed" the program to the Pascal language processor all at once, and then wait for the results. Often, when you type your program into the computer you aren't dealing with the Pascal processor at all; you use another program, a text editor, to let you enter your Pascal program into the computer. Then you start up Pascal itself. (Most microcomputer versions of Pascal include a simple text editor for program entry, just as Logo includes a procedure editor.) Typically you store your Pascal program as a file on a disk and you give the file name as input to the Pascal language processor.
Keep in mind that it's the process of writing and entering a program that's
non-interactive in Pascal. It's perfectly possible to write a Pascal program
that interacts with the user once it's running, alternating read and
write statements. (However, user input is one of the things I've left
out of my Pascal subset, as you'll see shortly.)
If you want to write your own Pascal programs for use with my compiler, you'll need a way to create a disk file containing your new program, using either Logo's procedure editor or some separate editing program. The sample Pascal programs in this chapter are included along with the Logo program files that accompany this book.
Our first example of a complete Pascal program is a version of the Tower of Hanoi puzzle. I described this problem in the first volume of this series. The Logo solution consists of two procedures:
to hanoi :number :from :to :other if equalp :number 0 [stop] hanoi :number-1 :from :other :to movedisk :number :from :to hanoi :number-1 :other :to :from end to movedisk :number :from :to print (sentence [Move disk] :number "from :from "to :to) end
To use these procedures you issue an instruction like
? hanoi 5 "a "b "c Move disk 1 from a to b Move disk 2 from a to c Move disk 1 from b to c Move disk 3 from a to b Move disk 1 from a to c ... and so on.
Here is the corresponding Pascal program. This program is in the
file tower. (As you can see, Pascal programs begin with a
program name; in all of the examples in this chapter the
file name is the same as the program name, although that isn't a requirement
of Pascal.) Never mind the program details for the moment; right now
the point is to make sure you know how to get the Pascal compiler to
translate it into Logo.
program tower;
{This program solves the 5-disk tower of hanoi problem.}
procedure hanoi(number:integer;from,onto,other:char);
{Recursive procedure that solves a subproblem of the original problem,
moving some number of disks, not necessarily 5. To move n disks, it
must get the topmost n-1 out of the way, move the nth to the target
stack, then move the n-1 to the target stack.}
procedure movedisk(number:integer;from,onto:char);
{This procedure moves one single disk. It assumes that the move is
legal, i.e., the disk is at the top of its stack and the target stack
has no smaller disks already. Procedure hanoi is responsible for
making sure that's all true.}
begin {movedisk}
writeln('Move disk ',number:1,' from ',from,' to ',onto)
end; {movedisk}
begin {hanoi}
if number <> 0 then
begin
hanoi(number-1,from,other,onto);
movedisk(number,from,onto);
hanoi(number-1,other,onto,from)
end
end; {hanoi}
begin {main program}
hanoi(5,'a','b','c')
end.
Once you have a Pascal program in a disk file, you compile it using the
compile command with the file name as input:
? compile "tower
The compiler types out the program as it compiles it, partly to keep you from falling asleep while it's working but also so that if the compiler detects an error in the program you'll see where the error was found.
When the compiler has finished processing the source file (the file containing the Pascal program) it stops and you see a Logo prompt. At this point the program has been translated into a simulated machine language. To run the program, say
? prun "tower Move disk 1 from a to b Move disk 2 from a to c Move disk 1 from b to c Move disk 3 from a to b Move disk 1 from a to c ... and so on.
The input to the prun (Pascal run) command is the program
name--the word that comes after program at the beginning of the
source file.
The difference between an interactive and a non-interactive language is not
just an arbitrary choice of "user interface" style. This choice reflects
a deeper distinction between two different ways of thinking about what
a computer program is.
In Logo there is really no such thing as a "program." Each procedure is an
entity on its own. You may think of one particular procedure as the
top-level one, but Logo doesn't know that; you could invoke any procedure
directly by using an interactive instruction naming that procedure. Logo
does have the idea of a workspace, a collection of procedures stored
together in a file because they are related. But a workspace
need not be a tree-structured hierarchy with one top-level procedure and the
others as subprocedures. It can be a collection of utility procedures with
no top-level umbrella, like the Berkeley Logo library.
It can be a group of projects that are conceptually related but with several
independent top-level procedures, like the two memoization examples, the two
sorting algorithms, the tree data base, and other projects in the algs
workspace of Chapter 3.
By contrast, a Pascal program is considered a single entity. It always
begins with the word program and ends with a period, by analogy with
an English sentence. (The subprocedures and the individual statements
within the program are separated with semicolons because they are analogous
to English clauses.*) It makes no sense to give the
Pascal compiler a source file containing just procedures without a main
program.
*I say "English" because I am writing for an
English-speaking audience, but in fact Pascal was designed by a largely
European committee including native speakers of several languages; principal
designer Niklaus Wirth is Swiss. Their languages all
have periods and semicolons, though.
Why did Logo's designers choose an interactive program development approach, while Pascal's designers chose a whole-program paradigm? Like all worthwhile questions, this one has more than one answer. And like many questions in language design, this one has two broad kinds of answer: the answers based on the implementation strategy for the language and the ones based on underlying programming goals.
The most obvious answer is that Pascal is a compiled language and Logo is an interpreted one. That is, most Pascal language processors are compilers: programs that translate a program from one language into another, like translating a book from English into Chinese. Most compilers translate from a source language like Pascal into the native machine language of whatever computer you're using. (My Pascal compiler translates into a simulated machine language that's actually processed by Logo procedures.) By contrast, most Logo versions are interpreters: programs that directly carry out the instructions in your source program, without translating it to a different ("object") language.*
*This is another
case in which the same word has two unrelated technical meanings. The use of
"object" in describing the result of a compilation (object program, object
language) has nothing to do with object-oriented programming.
To understand why interpreters tend to go with interactive languages, while compilers usually imply "batch mode" program development, think about the "little person" metaphor that's often used in teaching Logo. If you think of the computer as being full of little people who know how to carry out the various procedures you've written, the one who's really in charge is not the one who carries out your top-level procedure, but rather the one representing the Logo interpreter itself. If the procedure specialists are like circus performers, the Logo interpreter is the ringmaster. The circus metaphor is actually a pretty good one, because on the one hand each performer is an autonomous person, but at the same time the performers have to cooperate in order to put on a show. The relevance of the metaphor to this discussion is that in a compiled language there is no "ringmaster." The compiler is more closely analogous to a bird that hatches an egg (your program) and then pushes the new bird out of the nest to fend for itself. In a compiled language there is no provision for an interactive interface to which you can give commands that control the running of your program, unless your program itself includes such an interface.
Saying the same thing in a different way, the Logo interpreter is part of
the environment in which any Logo program operates. (That's why Logo can
provide a facility like the run command to allow your program to
construct new Logo instructions as it progresses.) But a Pascal compiler
does its job, translating your program into another form, and then
disappears. Whatever mechanisms are available to control your program have
to be built into the program. For example, my Pascal version of the Tower
of Hanoi program includes the top-level instruction that starts up the
solution for five disks. In the Logo version, that instruction isn't
considered part of the program; instead, you direct Logo interactively
to invoke the hanoi procedure.
The distinction between compiled and interpreted languages is not as
absolute as it once was. There are versions of Logo in which each procedure
is compiled as you define it, but it's still possible to give instructions
interactively. (Some such versions include both a compiler and an
interpreter; in others, the "interpreter" just arranges to compile each
instruction you type as if it were a one-line program.) And many current
Pascal compilers don't compile into the machine language of the host
computer, but rather into an intermediate language called
"P-code" that is then interpreted by another program, a
P-code interpreter. P-code is called an intermediate language
because the level of detail in a P-code program is in between that of a
language you'd want to use and that of the underlying machine language. Its
primitives are simple and quick, not complex control structures like
if or for. The advantage of a Pascal language processor based on
P-code is that the compiler is portable--it can work on
any computer. All that's needed to start using Pascal on a new computer is a
P-code interpreter, which is a relatively easy programming project.
So far I've been explaining a language design decision (interactive or non-interactive development) in terms of an implementation constraint (interpreted or compiled). But it's possible to look beyond that explanation to ask why someone would choose to design a compiler rather than an interpreter or vice versa.
The main advantage of a compiler is that the finished object program runs fast, since it is directly executed in the native language of the host computer. (An interpreter, too, ultimately carries out the program in the computer's native language. But the interpreter must decide which native language instructions to execute for a given source language instruction each time that instruction is evaluated. In a compiled language that translation process happens only once, producing an object program that requires no further translation while it's running.) The tradeoff is that the compilation process itself is slow. If you're writing a program that will be used every day forever, the compiled language has the advantage because the development process only happens once and then the program need not be recompiled. On the other hand, during program development the compiled language may be at a disadvantage, because any little change in one instruction requires that the entire program be recompiled. (For some languages there are incremental compilers that can keep track of what part of the program you've changed and only recompile that part.)
A compiled language like Pascal (or Fortran or C), then, makes sense in a business setting where a program is written for practical use, generally using well-understood algorithms so that the development process should be straightforward. An interpreted language like Logo (or Lisp or BASIC) makes more sense in a research facility where new algorithms are being explored and the development process may be quite lengthy, but the program may never be used in routine production. (In fact nobody uses BASIC for research purposes, because of other weaknesses, but its interactive nature is a plus.) Another environment in which interaction is important is education; a computer science student writes programs that may never actually be run except for testing. The program is of interest only as long as it doesn't work yet. For such programs the speed advantage of a compiled program is irrelevant.
There are also reasons that have nothing to do with implementation issues. I've spoken earlier of two conflicting views of computer science, which I've called the software engineering view and the artificial intelligence view. In the former, the program development process is seen as beginning with a clear, well-defined idea of what the program should do. This idea is written down as a program specification that forms the basis for the actual programming. From that starting point, the program is developed top-down; first the main program is written in terms of subprocedures that are planned but not written yet; then the lower-level procedures are written to fill in the details. No procedure is written until it's clear how that procedure fits into a specific overall program. Since Pascal's developers are part of the software engineering camp, it's not surprising that a Pascal program takes the form of an integrated whole in which each procedure must be inside a larger one, rather than a collection of more autonomous procedures. By contrast, Logo is a product of the artificial intelligence camp, for whom program development is a more complicated process involving bottom-up as well as top-down design. AI researchers recognize that they may begin a project with only a vague idea of what the finished program will do or how it will be organized. It's appropriate, then, to start by writing program fragments that deal with whatever subtasks you do understand, then see how those pieces can fit together to complete the overall project. Development isn't a straight line from the abstract specification to the concrete subprocedures; it's a zigzag path in which the programmer gets an idea, tries it out, then uses the results as the basis for more thinking about ideas.
Traditionally, an interpreter has been the primary tool to facilitate
interactive program development. Recently, though, software developers
have brought a more interactive flavor to compiled languages by inventing
the idea of an integrated development environment (IDE), in which a
compiler is one piece of a package that also includes a language-specific
editor (one that knows about the syntax of the language and automatically
provides, for example, the keyword do that must follow a for in
Pascal), online documentation, and a debugger, which is a program
that permits you to follow the execution of your program one step at a time,
like the step command in Berkeley Logo. The idea is to have your cake
and eat it too: You use the IDE tools during program development, but once
your program is debugged, you're left with a fast compiled version that can
be run without the IDE.
So far we've been looking at how each language thinks about a program as a whole. We turn now to the arrangement of pieces within a program or a procedure.
A Logo procedure starts with a title line, followed by the
instructions in the procedure body and then the end line.
The purpose of the title line is to give names to the procedure itself and
to its inputs.
The structure of a Pascal program is similar in some ways, but with some
complications. The program starts with a header line, very much
analogous to the title line in Logo. The word tower in the
header line of our sample program is the name of the program. Skipping
over the middle part of the program for the moment, the part between
begin and end in the last few lines is
the statement part of
the program, just as in Logo. The word end in the Pascal program is
not exactly analogous to the end line in a Logo procedure; it's a kind
of closing bracket, matching the begin before it. The period right
after the final end is what corresponds to the Logo end line.
What makes Pascal's structure different from Logo's is the part I've skipped
over, the declaration of procedures. In Logo, every procedure is a separate
entity. In Pascal, the declaration of the procedure hanoi, for
example, is part of the program tower. This particular
program uses no global variables, but if it did, those variables would also
have to be declared within the program. If the program used global
variables a, b, i, and j then it might begin
program tower;
var a,b:real;
i,j:integer;
procedure hanoi(number:integer;from,onto,other:char);
In summary, a Pascal program consists of
| 1. | the header line | |
|---|---|---|
| 2. | the declaration part (variables and procedures) | |
| 3. | the statement part | |
| 4. | the final punctuation (period) |
But notice that the procedure hanoi, declared inside
tower, has the same structure as the entire program. It
begins with a header line; its declaration part includes the declaration of
procedure movedisk; it has a statement part between begin and
end; its final punctuation is a semicolon instead of a period.
What does it mean for one procedure to be declared inside another?
You already know what a local variable means; if a variable v
belongs to a procedure p then that variable exists only while the
procedure is running; at another point in the program there might be a
different variable with the same name. In Pascal, the same is true for
local procedures. In our example program, the procedure movedisk
exists only while procedure hanoi is running. It would be an error to
try to invoke movedisk directly from the main program.
The header line for a procedure can include names for its inputs, just as the title line of a Logo procedure names its inputs. A useful bit of terminology is that the variable names in the procedure header are called formal parameters to distinguish them from the expressions that provide particular input values when the procedure is actually invoked; the latter are called actual arguments. The words "parameter" and "argument" are both used for what we call an "input" in Logo.*
*I'm misleading you a little bit by calling it a
"header line." Like any part of a Pascal program, the header can extend
over more than one line, or can be on the same line with other things. The
end of the header is marked with a semicolon. In Pascal a line break is
just like a space between words. However, there are conventions for
properly formatting a Pascal program. Even though the Pascal compiler
doesn't care about spacing and line breaks, people always do it as I've
shown you here, with subordinate parts of the program indented and each
statement on a separate line.
The sequence of header, declarations, statements, and punctuation is called a block. Pascal is called a block structured language because of the way blocks can include smaller blocks. Another aspect of block structure is Pascal's use of compound statements. A sequence of the form
begin statement ; statement ; statement end
is called a compound statement. An example from the tower
program is
begin hanoi(number-1,from,other,onto); movedisk(number,from,onto); hanoi(number-1,other,onto,from) end
(Notice that semicolons go between statements within this sequence; none is needed after the last statement of the group. This syntactic rule is based on the analogy between Pascal statements and English clauses that I mentioned earlier.) For example, Pascal includes a conditional statement whose form is
if condition then statement
The "statement" part can be a single simple statement,
like a procedure call, or it can be a compound statement delimited by
begin and end. Because the general term "block structured language"
refers to any syntactic grouping of smaller units into a larger one,
including compound statements, you may hear the word "block" used to refer
to a compound statement even though that's not the official Pascal meaning.
In Logo we don't talk about different kinds of statements like compound,
simple, and so on. Every Logo instruction (well, all but to)
is a procedure invocation. If, for example, is a procedure whose
first input is true or false and whose second input is a list
containing instructions to be carried out if the first input is true.
In Pascal there are several different kinds of statements, each with its own
syntax.
You know about compound statements. You've seen one example of if,
which is one of several structured statements in Pascal. Other
examples include
while condition do statement;
repeat statements until condition
while x < 0 do
begin
increase(x);
writeln(x)
end;
repeat
increase(x);
writeln(x)
until x >= 0;
These are like the while and do.until tools in
Berkeley Logo. While, like if, requires a single statement
(which can be a compound statement between begin and end) after
the do. However, the words repeat and until implicitly
delimit a compound statement, so you can put more than one statement between
them without using begin and end. Another example is
for, which you'll see in use in a moment. Continuing the analogy
with English grammar, a compound statement is like a compound sentence with
several independent (or coordinate) clauses; a structured statement is like
a complex sentence, with a dependent (or subordinate) clause. (If you
always hated grammar, you can just ignore this analogy.)
There are basically only two kinds of simple statement: the
procedure call,
which you've already seen, and the assignment statement used to give
a variable a new value. This latter is Pascal's version of make in
Logo; it takes the form
variable := expression slope := ychange/xchange
As I've already mentioned, the variable must have been declared
either in a procedure heading or in a var declaration.
(Assignment is represented with the two-character symbol := because
= by itself means equalp rather than make.)
I say there are "basically" only two kinds because each of these has some
special cases that look similar but follow different rules. For example,
printing to the computer screen is done by what looks like an invocation of
write (analogous to type in Logo) or
writeln ("write line," analogous to print). But these are
not ordinary procedures. Not only do they take a variable number of
arguments, but the arguments can take a special form not ordinarily
allowed. In the movedisk procedure in the tower program, one of
the arguments to writeln is
number:1
The ":1" here means "using one print position unless more
are needed to fit the number." Pascal print formatting is designed to
emphasize the printing of numbers in columns, so the default is to print
each number with a fairly large number of characters, with spaces at the
left if the number doesn't have enough digits. The exact number of
characters depends on the type of number and the dialect of Pascal, but 10
is a typical number for integers. So
writeln(1,2,3,4); writeln(1000,2000,3000,4000);
will give a result looking something like this:
1 2 3 4
1000 2000 3000 4000
In movedisk I had to say ":1" to avoid all that
extra space.
What are the pros and cons of using a variety of syntax rules for different kinds of statements? One reason for the Pascal approach is that differences in meaning can be implicit in the definitions of different statement types instead of having to be made explicit in a program. Don't worry; you're not expected to understand what that sentence meant, but you will as soon as you see an example. In Logo we say
if :x < 10 [increment "x] while [:x < 10] [increment "x]
Why is the predicate expression :x < 10 in a quoted list in
the case of while but not for if? If wants the
expression to be evaluated once, before if is invoked. The
actual input to if is not that expression but the value of the
expression, either true or false. While, on the other
hand, wants to evaluate that expression repeatedly. If Logo evaluated the
expression ahead of time and gave while an input of true or
false it wouldn't be able to know when to stop repeating.
The fact that if wants the condition evaluated once but while
wants to evaluate it repeatedly has nothing to do with the syntax of Logo;
the same is true in Pascal. But in Pascal you say
if x<10 then increment(x); while x<10 do increment(x);
In Logo the fact that if's condition is evaluated in advance
but while's isn't is made explicit by the use of square brackets. In
Pascal it's just part of the semantic definitions of the if
and while statements. (Syntax is the form in which something
is represented; semantics is the meaning of that something.)
One more example: Beginning students of Logo often have trouble understanding why you say
make "new :old
to assign the value of one variable to another variable. Why is
the first quoted and the second dotted? Of course you understand that it's
because the first input to make is the name of the variable
you want to set, while the second is the value that you want to give
it. But in Pascal this distinction is implicit in the semantic definition
of the assignment statement; you just say
new := old
Since beginning Logo students have trouble with quotes and dots in
make, you might think that the Pascal approach is better. But beginning
Pascal students have a trouble of their own; they tend to get thrown by
statements like
x := x+1
This doesn't look quite as bad as the BASIC or Fortran version in
which the symbol for assignment is just an equal sign, but it's still easy
to get confused because the symbol "x" means two very different
things in its two appearances here. In the Logo version
make "x :x+1
the explicit difference in appearance between "x and :x
works to our advantage.
Which way do you find it easier to learn something: Do you want to start with a simple, perhaps partly inaccurate understanding and learn about the difficult special cases later, or do you prefer to be told the whole truth from the beginning? I've posed the question in a way that shows my own preference, I'm afraid, but there are many people with the opposite view.
The issue about whether or not to make the semantics of some action implicit
in the syntax of the language is the most profound reason for the difference
between Logo's single instruction syntax and Pascal's collection of
statement types, but there are other implications as well. One virtue of
the Pascal compound statement is that it makes for short, manageable
instruction lines. You've seen Logo procedures in these books in which one
"line" goes on for three or four printed lines on the page, e.g., when the
instruction list input to if contains several instructions. It's a
particularly painful problem in the versions of Logo that don't allow
continuation lines.
On the other hand, Logo's syntactic uniformity contributes to its
extensibility. In the example above, if is a Logo primitive,
whereas while is a library procedure written in Logo. But the
difference isn't obvious; the two are used in syntactically similar ways.
You can't write control structures like while in Pascal because
there's nothing analogous to run to allow a list of instructions to be
an input to a procedure, but even if you could, it would have to take the
form
while(condition,statement)
because that's what a procedure call looks like. But it's not what a built-in Pascal control structure looks like.
It's time for another sample Pascal program. Program cards is a
Pascal version of the problem of shuffling a deck of cards that we discussed
in Chapter 3. It includes local variables, assignment statements, and the
for structured statement. It also will lead us into some
additional language design issues.
program cards;
{Shuffle a deck of cards}
var ranks:array [0..51] of integer;
suits:array [0..51] of char;
i:integer;
procedure showdeck;
{Print the deck arrays}
begin {showdeck}
for i := 0 to 51 do
begin
if i mod 13 = 0 then writeln;
write(ranks[i]:3,suits[i]);
end;
writeln;
writeln
end; {showdeck}
procedure deck;
{Create the deck in order}
var i,j:integer;
suitnames:packed array [0..3] of char;
begin {deck}
suitnames := 'HSDC';
for i := 0 to 12 do
for j := 0 to 3 do
begin
ranks[13*j+i] := i+1;
suits[13*j+i] := suitnames[j]
end;
writeln('The initial deck:');
showdeck
end; {deck}
procedure shuffle;
{Shuffle the deck randomly}
var rank,i,j:integer;
suit:char;
begin {shuffle}
for i := 51 downto 1 do {For each card in the deck}
begin
j := random(i+1); {Pick a random card before it}
rank := ranks[i]; {Interchange ranks}
ranks[i] := ranks[j];
ranks[j] := rank;
suit := suits[i]; {Interchange suits}
suits[i] := suits[j];
suits[j] := suit
end;
writeln('The shuffled deck:');
showdeck
end; {shuffle}
begin {main program}
deck;
shuffle
end.
Experienced Pascal programmers will notice that this program isn't written in the most elegant possible Pascal style. This is partly because of issues in Pascal that I don't want to talk about (records) and partly because of issues that I do want to talk about in the next section (scope).
Here's what happens when you run the program:
? prun "cards The initial deck: 1H 2H 3H 4H 5H 6H 7H 8H 9H 10H 11H 12H 13H 1S 2S 3S 4S 5S 6S 7S 8S 9S 10S 11S 12S 13S 1D 2D 3D 4D 5D 6D 7D 8D 9D 10D 11D 12D 13D 1C 2C 3C 4C 5C 6C 7C 8C 9C 10C 11C 12C 13C The shuffled deck: 2D 11D 6S 9D 6C 10H 8D 11C 3D 4C 5H 4S 1D 5C 5D 6D 9S 4D 8C 13S 13D 10C 9H 10D 5S 12D 13H 9C 3C 1S 10S 4H 12S 11S 12H 11H 2H 3H 1H 13C 8H 7C 2C 1C 7S 6H 2S 7D 8S 12C 3S 7H
The Pascal for is somewhat like the Berkeley Logo for
in its semantics, although of course the syntax is quite different. The
step value must be either 1 (indicated by the keyword to) or −1
(downto). By the way, if you've been wondering why I changed one of
the variable names in the Tower of Hanoi program from to in the Logo
version to onto in the Pascal version, it's because to is a
reserved word in Pascal and can't be used as the name of
anything.
The Pascal standard does not include a random function. Most
practical versions of Pascal do provide a random number generator of some
sort; since there's no standard, I've chosen to implement the kind that's
most useful for the kind of programming I'm interested in, namely the Logo
random that takes an integer argument and returns an integer between
zero and one less than the argument.
Program cards has three procedures: showdeck, deck,
and shuffle. Each of these is declared directly in the top-level
program. However, showdeck is not invoked directly at top
level; it's used by the other two procedures. (This is one of the
questionable bits of programming style I've put in for the sake of the
following discussion; ordinarily I think I'd have put the statements that
invoke showdeck in the main program block.)
If you read the program carefully you'll see that showdeck uses a
variable i but does not declare that
variable.* (When a
variable is used but not declared within a certain procedure, that use of
the variable is called a free reference. A use of a
variable that
is declared in the same block is called a bound reference.)
There are three variables named i in the program: one in the outer
block, one in deck, and one in shuffle. When, for example, the
main program calls deck and deck calls showdeck, which
variable i does showdeck use?
*Actually, the Pascal language requires that the variable
used in a
for statement must be declared in the same procedure
in which the for appears; program cards is not legal Pascal for
that reason. What's the purpose of that restriction? Suppose that this
procedure was invoked from within another for loop in another
procedure, and both use the same variable; then both procedures would be
trying to assign conflicting values to that variable. Berkeley Logo's
for automatically makes its variable local to the for procedure
itself, for the same reason. But my Pascal compiler lets us get away with
breaking this rule, and I've done it deliberately to make a point.
In Logo the answer would be that showdeck uses the i belonging
to deck, the procedure that invoked it. That's because Logo follows
the rules of dynamic scope: A free reference to a variable is
directed to the variables of the procedure that invoked the current one,
then if necessary to the variables of the procedure that invoked that one,
and so on up to the global variables. (Dynamic scope is discussed more
fully in the first volume of this series.)
In Pascal, showdeck uses the i belonging to the main program.
That's because a free reference to a variable is directed to the block
within which the current procedure was declared, then to the block
surrounding that one, and so on up to the outermost program block. This
rule is called lexical scope. The set of blocks surrounding a
given block, smaller to larger, is its lexical environment. The
lexical environment of showdeck is
{showdeck, cards}
The lexical environment of movedisk in the tower
program is
{movedisk, hanoi, tower}
The set of procedure invocations leading to a given procedure is
its dynamic environment. A procedure's dynamic environment
isn't always the same; for example, the dynamic environment of
showdeck is sometimes
{showdeck, deck, cards}
and sometimes
{showdeck, shuffle, cards}
The word "lexical" is the adjective form of lexicon, which means "dictionary." It's used in this computer science context because the lexical context of a procedure has to do with where it's defined, just as words are defined in a dictionary. The word "dynamic" means in motion; it's used because the dynamic context of a procedure keeps changing as the program runs.
What are the reasons behind the choice of lexical or dynamic scope? This is another choice that was originally made for implementation reasons. It turns out to be easy for an interpreter to use dynamic scope, but for a compiler it's much easier to use lexical scope. That's because the interpreter makes the decision about which variable to use while the program is running and the dynamic environment is known, but the compiler has to translate the program before it is run. At "compile time" there isn't one fixed dynamic environment, but there is a single, already-known lexical environment. Originally, interpreted languages like Logo, Lisp, and APL all used dynamic scope, while compiled ones like Fortran and Pascal used lexical scope. (There was even a period of time when Lisp systems offered both an interpreter and a compiler, and the behavior of the same program was different depending on whether you compiled it or interpreted it because of different scope rules.)
More recent dialects of Lisp, such as Common Lisp and Scheme, have been
designed to use lexical scope even when interpreted. Their designers
think lexical scope is better for reasons that don't depend on the
implementation technique. One reason is that dynamic scope allows for
programming errors that don't arise when lexical scope is used. In Logo,
suppose you write a procedure that makes a free reference to some variable
v. What you intended, let's say, was to use a global variable by that
name. But you've forgotten that your procedure is sometimes invoked by
another procedure that you wrote two weeks ago that happens to have an input
named v. It can be very hard to figure out why your procedure is
suddenly getting the wrong variable. With lexical scope, it's much easier
to keep track of the context in which your procedure is defined, to make
sure there are no local variables v in the lexical environment.
It's possible to argue in favor of dynamic scope also. One
argument is that in a lexically scoped language certain kinds of tool
procedures can't be written at all: the ones like while or for
that take an instruction list as input and run the list repeatedly.
Suppose you write a procedure in Logo that contains an instruction like
while [:degrees < 0] [make "degrees :degrees+360]
What variable degrees do you want this instruction to use?
Presumably you mean the same variable degrees that is used by other
instructions in the same procedure. But if Logo used lexical scope,
then while wouldn't have access to the local variables of your
procedure. (It's possible to design other features into a lexically scoped
language to get around this limitation, but the necessary techniques are
more complicated than the straightforward way you can write while in
Logo.)
Another argument for dynamic scope, with particular relevance to Logo, is
that dynamic scope fits better with the expectations of an unsophisticated
programmer who hasn't thought about scope at all. One of the design goals
of Logo is to be easy for such beginners. Until now we've been talking
about scope in terms of naming conflicts: what happens if two variables have
the same name. But suppose you write a program with a bunch of procedures,
with a bunch of distinct variable names used as inputs. It makes
life very simple if all those variables are available whenever you want them,
so you don't have to think in such detail about how to get a certain piece
of information down the procedure invocation chain to a subprocedure. If
some variables are accessible to subprocedures but others aren't, that's one
more mystery to make programming seem difficult. In particular, dynamic
scope can simplify the debugging of a Logo program. If you arrange for your
program to pause at the moment when an error happens, then you can
enter Logo instructions, with all of the local variables of all
pending procedure invocations available, to help you figure out the reason
for the error. Debuggers for lexically scoped languages require a more
complicated debugging mechanism in which the programmer must explicitly
shift focus from one procedure to another.
In the situations we've seen, lexical scope always acts as a
restriction on the availability of variables to subprocedures. That is,
a procedure's lexical environment is always a subset of its dynamic
environment. (Suppose procedure a includes the definition of
procedure b, which in turn includes the definition of c. So the
lexical environment of c is {c,b,a}. You might imagine that
c's dynamic environment could be {c,a} if procedure a
invoked c directly, but in fact that's illegal. Just as a can't
use b's local variables, it can't use b's local procedures
either. The reason the dynamic environment can be different from the
lexical one at all is that two procedures can be part of the same block,
like showdeck and deck in the cards program.) In Lisp,
it's possible for a procedure to return another procedure as its
output--not just the name of the procedure or the text of the procedure, as
we could do in Logo, but the procedure itself, lexical environment and all.
When such a procedure is later invoked from some other part of the
program, the procedure's lexical environment may not be a subset
of its dynamic environment, and so lexical scope gives it access to
variables that it couldn't use under dynamic scope rules. That's a powerful
argument in favor of lexical scope for Lisp, but it doesn't apply to Pascal.
One special scope rule in Pascal applies to procedures declared in the same
block: The one declared later can invoke the one declared earlier, but not
the other way around. In the cards program, deck can call
showdeck but showdeck can't call deck. There is no deep reason
for this restriction; it's entirely for the benefit of the compiler. One of
the design goals of Pascal was that it should be easy to write a compiler
that goes through the source program once, from beginning to end, without
having to back up and read part of the program twice. In particular, when
the compiler sees a procedure invocation, it must already know what inputs
that procedure requires; therefore, it must have already read the header of
the subprocedure. Usually you can get around this restriction by rearranging
the procedures in your program, but for the times when that doesn't work
Pascal provides a kludge that lets you put the header in one place in the
source file and defer the rest of the procedure until later.
Berkeley Logo has three data types: word, list, and array. (Numbers are just words that happen to be full of digits.) But a variable in Logo does not have a type associated with it; any datum can be the value of any variable.
Pascal has lots of types, and every variable belongs to exactly one of them. In the sample programs so far we've used five types: char, integer, array of char, array of integer, and packed array of char. When a variable is declared, the declaration says what type it is.
The selection of data types is the area in which my Pascal compiler is most lacking; I've implemented only a few of the possible types. I'll describe the ones available in my compiler in detail and give hints about the others.
The fundamental types out of which all others are built are the scalar types that represent a single value, as opposed to an aggregate like an array or a list. Pascal has four:
integer | a positive or negative whole number (e.g.,
23)
| |
|---|---|---|
real | a number including decimal fraction part (e.g.,
-5.0)
| |
char | a single character (e.g., 'Q')
| |
Boolean | true or false
|
Pascal also has several kinds of aggregate types. The only one that I've implemented is the array, which is a fixed number of uniform elements. By "uniform" I mean that all members of the array must be of the same type. Full Pascal allows the members to be of any type, including an aggregate type, as long as they're all the same, so you could say
var a : array [1..10] of array [1..4] of integer;
to get an array of arrays. But in my subset Pascal the members of an array must be scalars. This restriction is not too severe because Pascal arrays can have multiple indices; instead of the above you can use the equivalent
var a : array [1..10, 1..4] of integer;
This declaration creates a two-dimensional array whose members
have names like a[3,2].
The notation 1..10 is called a range; it indicates the extent
of the array. Berkeley Logo arrays ordinarily start with index one, so
a Logo instruction like
make "ten array 10
is equivalent to the Pascal declaration
var ten:array [1..10] of something
except that the Logo array need not have uniform members.* (Also, a subtle difference is that the Logo array is an independent datum that can be the value of a variable just as a number can be the value of a variable. The Pascal array is the variable; you can change the contents of individual members of the array but it's meaningless to speak of changing the value of that variable to be something other than that array.)
*The Berkeley Logo
array primitive can take an optional
second input to specify a different starting index.
In Pascal an index range doesn't have to be numbers; you can use any scalar type except real:
var frequency : array ['a'..'z'] of integer;
might be used in a program that counts the frequency of use of
letters, such as a cryptography program. The members of this array would be
used by referring to things like frequency['w']. (In Pascal
documentation there is a word for "scalar type other than real": It's
called an ordinal type.)
A packed array is one that's represented in the computer in a way that takes up as little memory as possible. Ordinary arrays are stored so as to make it as fast as possible to examine or change an individual element. The distinction may or may not be important for a given type on a given computer. For example, most current home computers have their memory organized in bytes that are just the right size for a single character. On such a computer, an array of char and a packed array of char will probably be represented identically. But one of my favorite larger computers, the Digital Equipment Corporation PDP-10, had its memory organized in words of 36 bits, enough for five 7-bit characters with one bit left over. A packed array of char, on the PDP-10, would be represented with five characters per word; an ordinary array of char might store only one character per word, wasting some space in order to simplify the task of finding the nth character of the array.
My compiler, which is meant to be simple rather than efficient, ignores the
packed declaration. The reason I used it in the cards program
is to illustrate a rule of Pascal: The statement
suitnames := 'HSDC'
assigns a constant string to the array variable
suitnames, and such assignments are allowed only to packed arrays of char.
Also, the size of the array must equal the length of the string. If
suitnames were an array of length 10, for example, I'd have had to say
suitnames := 'HSDC '
filling up the unused part of the array explicitly with spaces.
In an assignment statement, the type of the variable on the left must be the same as the type of the expression on the right. An assignment can copy one array into another if it involves two variables of exactly the same type:
var a,b:array [3..17] of real; a := b
but except for the case of packed arrays of char mentioned above there is no way to represent a constant array in a Pascal program. If you want an array of all the prime numbers less than 10 you have to initialize it one member at a time:
var primes : array [1..4] of integer; primes[1] := 2; primes[2] := 3; primes[3] := 5; primes[4] := 7
In scalar assignments, a slight relaxation of the rules is allowed in that
you may assign an integer value to a real variable. The value is converted
to a real number (e.g., 17 to 17.0). The opposite is
not allowed, but there are two built-in functions trunc (for
"truncate") and round that can be used to convert a real value to an
integer. Trunc cuts off the fraction part, so trunc(4.99) is
4. Round rounds to the nearest integer.
Pascal provides the usual infix arithmetic operations +, -,
*, and /, following the usual precedence rules, just as in Logo.
The result of any of these is integer if both operands are integer,
otherwise real, except that the result of / (division) is always real.
There are integer division operations div (integer quotient) and
mod (integer remainder); both operands to these must also be integers.
The relational operators = (like equalp in Logo), < (less
than), > (greater than), <= (less than or equal to), >=
(greater than or equal to), and <> (not equal to) take two real or
integer operands and yield a Boolean result. There are also Boolean
operators and, or, and not, just like the Logo ones except
that they use infix syntax:
(x < 0) and (y <= 28)
Standard Pascal, but not my version, includes other aggregate types besides
the array. One such type is the record; a record is a non-uniform
aggregate, but the "shape" of the aggregate must be declared in advance.
For example, you can declare a record containing three integers and an array
of 10 characters. In the cards program, instead of two separate
arrays for ranks and suits I could have said
var carddeck: array [0..51] of record
rank:integer;
suit:char
end;
Then to refer to the rank of card number 4 I'd say
carddeck[4].rank
and that would be an integer. A pointer is a variable whose value is the memory address of a record; pointer variables can be used to implement dynamic data structures like Logo lists by building explicitly the collections of boxes and arrows illustrated in some of the pictures in Chapter 3. But it's hard to build anything in Pascal that's quite like Logo lists, even using pointers, because what's in each box has to belong to some particular predeclared type.
Real Pascal also includes user-defined types. There is a
type
declaration that goes before the var declaration in a block:
type string = packed array [1..10] of char;
Variable declarations can then use string as the type of the
variable being declared. In fact, standard Pascal requires the use
of named types in certain situations. For example, in a procedure header
the formal parameters must be given a named type (either a built-in scalar
type like integer or a defined type like string); since I haven't
implemented type my compiler allows
procedure paul(words:packed array [1..10] of char);
although standard Pascal doesn't allow such a header.
You can also define subrange types:
type dieface = 1..6;
This type is really an integer, but it's constrained to have only values in the given range. This particular one might be used for a variable whose value is to represent the result of rolling a six-sided die. Finally, there are enumerated types:
type Beatle = (John, Paul, George, Ringo);
This type is used for a variable that represents one of a small
number of possible things. In reality it's also a kind of integer; the word
John represents 0, Paul is 1, and so on. In fact, it's only
during the compilation of the program that Pascal remembers the names of the
possible values; you can't read or print these variables during the running
of the program.
Why would anyone want to use a subrange or other restricted type? If the
program works using a variable of type dieface, it would work just as
well if the variable were of type integer. The only difference is
that using a subrange type is slower because the program has to check (at
run time) to make sure that any value you try to assign to that variable is
in the approved range.
According to Pascal enthusiasts, the virtue of restricted types, like the
virtue of typed variables in the first place, is that their use helps catch
program bugs. For example, in the cards program, procedure
shuffle has variables i and j that are used to index the arrays
ranks and suits. How do we know there isn't an error in the
program so that one of those variables is given a value that isn't a valid
index for those arrays? Such an error would be caught when we use
the index variable to try to refer to an array element that doesn't exist,
but it's easier to debug the program if we get the error message at the
moment when the variable is assigned the incorrect value. So I should have
declared
var i,j : 0..51;
instead of using integer. (Of course one reason I didn't
use a subrange type is that I didn't implement them in my compiler!)
The trouble is that strict typing of variables is an unnecessary pain in the neck.* Take this business of array index bounds. Here is a possible piece of Pascal program:
*I know I said I wasn't going to try to convince you which
language is better, but on this particular point I really think the Pascal
people don't have a leg to stand on.
i := 0;
while i <= 51 do
begin
writeln(ranks[i]:3,suits[i]);
i := i+1
end
There's nothing wrong with this. It will print the value of each
member of the two arrays, starting from index 0 and continuing through 51.
However, at the end of the while statement, the variable i has
the value 52. This is not an error; the program does not try
to refer to member 52 of the arrays. But if we declared i as a
subrange type the way we "should," the program will give an error message
and die. This particular example could be rewritten using for instead
of while to avoid the problem, but it turns out that there are many
algorithms that jump around in an array in which the index variable
sometimes takes on a value just outside the bounds of the array. Some sort
algorithms, for example, are like that.
Typed variables work against program robustness. (A robust program
is one that keeps calm in the face of bad data or other user error, rather
than dying abruptly.) For example, suppose we want to find the sum of a
bunch of numbers. Some human being is going to type these numbers into the
computer, one at a time. We don't know in advance how many there are, so we
let the person type done when done. Since the typist is only human,
rather than a computer, we want to make sure the program doesn't blow up if
he accidentally types something other than a number or done. Here's
one way to do it in Logo:
to addnumbers print [Enter the numbers, one per line.] print [Type the word 'done' when done.] print se [The sum is] addnumbers1 0 end to addnumbers1 :sum localmake "next readnumber if emptyp :next [output :sum] output addnumbers1 :sum+:next end to readnumber localmake "input readlist if emptyp :input [output readnumber] if equalp :input [done] [output []] if numberp first :input [output first :input] print [Please type numbers only.] output readnumber end
If the user makes a typing mistake, the program says so, ignores
the bad input, and keeps going. Now, how shall we write this in Pascal?
Into what type of variable should we read each number from the keyboard? If
we pick integer, then any entry of a non-number will incite Pascal to
print an error message and terminate the program. Instead we can read the
keyboard entry into an array of char, one character at a time. Then
anything the user types is okay, but we can't do arithmetic on the
result--we can't add it into the accumulated sum. We can read it as
chars and then write a procedure that knows how to look at a string of
digits and compute the number that those digits represent. But this is not
the sort of thing that we should need to do ourselves in a high-level
programming language.
Why should a programmer have to decide in advance whether or not the numbers that a program will manipulate are integers? In Logo I can write a general numeric procedure like this one:
to square :x output :x * :x end
but in Pascal I need one for each kind of number:
function RealSquare(x:real): real; begin RealSquare := x * x end; function IntSquare (x:integer): integer; begin IntSquare := x * x end;
Why pick on the distinction between integer and non-integer values? Why not positive and negative values, or odd and even values? The historical answer is that computer hardware uses two different representations for integer and real numbers, but so what? That doesn't mean the distinction is relevant to the particular program I'm writing.
The language ML, which I mentioned earlier as an example of a pure functional
language, tries to provide the best of both worlds on this issue. It does
require that variables have types, as in Pascal, to help catch programming
errors. But two features make ML's type system more usable than Pascal's.
One is the provision of union types. It's possible to say that
a particular variable must contain either a number or the word done,
for example. (Pascal has something like this, called variants, but
they're less flexible.) Second, the ML compiler uses type inference,
a technique by which the compiler can often figure out the appropriate type
for a variable without an explicit declaration.
In Logo a distinction is made between those procedures that output a value (operations) and those that don't (commands). Pascal has the same categories, but they're called functions and procedures respectively.
A function is a block just like a procedure block except for the minor changes needed to accommodate the fact that the function produces a value. First of all, the function header has to say what the type of the result will be:
function whatever (arguments) : integer;
The function's type must be a scalar, not an aggregate type. This restriction is in the standard only to make life easier for the compiler, and some versions of Pascal do allow array-valued (or record-valued, etc.) functions.
The other difference is that in the statement part of a function block we
have to tell Pascal what the value will be. That is, we need something
equivalent to output in Logo. Pascal's convention is that somewhere
in the block an assignment statement must be executed that has the
name of the function as its left hand side. That is, the function name is
used in an assignment statement as though it were a variable name.
(However, the name must not be declared as a variable.) This
notation may be a little confusing, because if the same name appears on the
right side of the assignment statement, it signals a recursive
invocation of the function. Perhaps an example will make this clear.
Program multi is a Pascal version of the memoized multinomial function
from Chapter 3. In the Logo version, t(n,k) was memoized using the
property name k on the property list named n. In the Pascal version,
since we have multi-dimensional arrays, it is straightforward to use a
two-dimensional array and store t(n,k) in memo[n,k].
program multi;
{Multinomial expansion problem}
var memo: array [0..4, 0..7] of integer;
i,j: integer;
function t(n,k:integer) : integer;
function realt(n,k:integer) : integer;
{without memoization}
begin {realt}
if k = 0 then
realt := 1
else
if n = 0 then
realt := 0
else
realt := t(n,k-1)+t(n-1,k)
end; {realt}
begin {t}
if memo[n,k] < 0 then
memo[n,k] := realt(n,k);
t := memo[n,k]
end; {t}
begin {main program}
{initialization}
for i := 0 to 4 do
for j := 0 to 7 do
memo[i,j] := -1;
{How many terms in (a+b+c+d)7?}
writeln(t(4,7));
end.
The assignment statements like
realt := 0
are the ones that control the values returned by the functions.
These assignment statements are not exactly like output in Logo
because they do not cause the function to return immediately. They act just
like ordinary assignments, as if there were actually a variable named
realt or t; when the statement part of the function is finished,
whatever value was most recently assigned to the function name is the one
that's used as the return value. (In fact the functions in program
multi are written so that only one such assignment is carried out, and
there are no more statements to execute after that assignment. That's a
pretty common programming style; it's rare to change the assignment to the
function name once it's been made.)
Apart from arbitrary syntactic details, Pascal's design with respect to procedures and functions is similar to Logo's, so I can't ask why the two languages made different choices. It's probably just as well, since you shouldn't get the impression that Pascal is the exact opposite of Logo in every way. Instead we could compare these two languages with Lisp, in which there are only operations, or most versions of BASIC, in which there are only commands. But I don't have the space to teach you enough about those languages to make such a comparison meaningful.
Consider this Logo procedure:
to increment :var make :var (thing :var)+1 end ? make "baz 23 ? increment "baz ? print :baz 24
The input to increment is the name of a variable
that you want to increment. A similar technique is used, for example, in
the push and pop library procedures, which take the name of a stack
variable as input. The reason this technique is necessary is that we want
the procedure to be able to modify the variable--to assign it a new value.
The same technique won't work in Pascal. For one thing, the association of
a name with a variable only exists at compile time. Once the compiled
program is running, the variables have no names, only addresses in computer
memory. Also, increment takes advantage of dynamic scope because the
variable it wants to modify isn't its own, but rather a variable accessible
to the calling procedure.
Here's how you do it in Pascal:
procedure increment(var v:integer);
begin
v := v+1;
end;
What's new here is the reserved word var in the argument
list. This word indicates that v is a variable parameter;
ordinary ones are called value parameters. Increment would be
used in a program like this:
program whatzit; var gub:integer; begin ... gub := 5; increment(gub); ... end.
Suppose increment had been written without the word var in its
header. In that case, when the statement increment(gub) was executed
here's what would happen. First, the actual argument to increment
(namely gub) would be evaluated. The value would be 5, since that's
the value of the variable gub. Then that value would be assigned to
the local variable v in increment. Then the instruction part of
increment would be run. The assignment statement there would change
the value of v from 5 to 6. Then increment would be finished,
and its local variable v would disappear. All of this would have no
effect on the variable gub. This ordinary interpretation of v
is called call by value because what gets associated with
the name v is the value of the actual argument, 5 in this
example, regardless of how that 5 was derived. For example, the instruction
in the main program could have been
increment(2+3);
and it wouldn't have mattered.
Making v a variable parameter instead of a value parameter changes the
operation of the program substantially. When increment is invoked,
the actual argument must be a variable name, not an arbitrary
expression. Pascal does not find the value of the actual argument and pass
that value along to increment; instead, the formal parameter
v becomes another name for the same variable named in the
actual argument. In this example, v becomes another name for
gub. So the assignment statement
v := v+1
isn't really about the local variable v at all; it's another
way to say
gub := gub+1
and so it does affect the variable in the calling block.
This use of variable parameters is called call by reference
because the formal parameter (v) refers to another variable.
One way to think about call by reference is that it provides, in effect, a
sort of limited dynamic scope. It's a way for a superprocedure to
allow a subprocedure access to one selected variable from the
superprocedure's lexical environment. Because this permission is
given to the subprocedure explicitly, call by reference doesn't give rise to
the possible naming bugs that argue against dynamic scope in general. Also,
dynamic scope as used in Logo has the problem that you have to be careful
not to allow a formal parameter name to be the same as the name of a
variable you want to use from the superprocedure's environment. For example,
in the Logo version of increment, what if you wanted to use
increment to increment a variable named var? If you try to say
increment "var
it won't work, because increment will end up trying to
increment its own formal parameter. (This is why the inputs to some of the
Berkeley Logo library procedures have such long, obscure names.) But the
Pascal increment would have no trouble with a variable named v
in the calling procedure.
On the other hand, call by reference is a little mysterious. If you've
understood all of the above, and you know exactly when you should say var
in a formal parameter list and when you shouldn't, you're doing better than
most beginning Pascal students. In Logo there is only one rule about
passing inputs to procedures; to make something like increment work,
you explicitly pass the name of a variable as input.
Call by reference is generally used when a subprocedure needs to change the value of a variable in a superprocedure. But there is also another situation in which some people use it. Suppose you want to write a procedure that takes a large array as an argument. If you make the array a value parameter, Pascal will allocate space for the array in the subprocedure and will copy each member of the array from the superprocedure's variable into the subprocedure's variable as the first step in invoking the subprocedure. This time-consuming array copying can be avoided by declaring the array as a variable parameter, thereby giving the subprocedure direct access to the superprocedure's array. Pascal enthusiasts consider this use of call by reference cheating, though, because it creates the possibility that the subprocedure could accidentally change something in the superprocedure's array. Call by value is safer, from this point of view.
Does Logo use call by value or call by reference for passing arguments to procedures? The official textbook answer is "call by value," but I find that misleading, because those two categories really make sense only in a language with a particular idea of what a variable is. A Logo variable is different from a Pascal variable in a subtle way. If you can understand this difference between the two languages, you'll have learned something very valuable.
In Logo, the world is full of data (words, lists, and arrays). These data may or may not be associated with variables. For example, when you enter an instruction like
print butlast butfirst [Yes, this is a list evidently.]
three different lists are involved: the one you typed explicitly in the instruction and two smaller lists. None of these three lists is the value of any variable. A variable is an association (called a binding) between a name and a datum. If you enter the instruction
make "langs [Logo Lisp APL]
we say that the name langs is bound to the indicated
list. If you then do
make "mylangs :langs
we say that the name mylangs is bound to the same
datum as langs. We're dealing with one list that has two names.
In Pascal a variable is not a binding in this sense. A Pascal variable is the datum it contains. If you have two array variables
var this,that: array [1..10] of integer;
and you do an assignment like
this := that;
then there are two separate arrays that happen to have
equal values stored in them. The same thing is true, although it's less
obviously meaningful, about scalars. If integer variables i and
j both have the value 10, then there are two different integers
that happen to have the same value. That's not the way a mathematician uses
the word "integer"; to a mathematician, there is only one 10. But to a
Pascal programmer, an integer isn't something like 10; an integer is a box,
and in the box there might be something like 10.
In Logo, a variable assignment (that is, an invocation of make)
changes the binding of the given variable name so that that name is
now associated with a different datum. In Pascal, a variable assignment
changes the value of the datum that is unalterably associated with
the named variable.
The official textbook story is this: A Logo variable is a box, just as a Pascal variable is a box. The difference is that what goes in the box, in Logo, is a pointer to the datum of interest. (A binding, officially, is the connection between the variable's name and its box. So there are two levels of indirection in finding what we ordinarily think of as the value of a variable: First the binding gets us from the name to a box--a location in the computer's memory--and then in that box we find a pointer, which gets us to another location in memory, which holds the actual information we want. In this model, call by reference can easily be described by saying that two different names are bound to the same box.) From this point of view, it makes sense to say that Logo uses call by value, because the "value" in question is the pointer, which is indeed copied when a procedure is called.
But ordinarily we don't think of the value of a Logo variable as being a
pointer; we think that the value of the variable is a word, a list, or an
array. From that point of view, parameter passing in Logo acts like call by
reference in some ways but like call by value in other ways. For example,
call by value makes a copy of the datum being passed. Logo does not copy
the actual datum, so in that respect it's like call by reference. On the
other hand, assigning a new value to a Logo formal parameter does not change
the value of any variables in the calling procedure; in that way, Logo works
like call by value. On the third hand, if the datum to which the formal
parameter is bound is a mutable data structure, such as an array, a
Logo subprocedure can change the value of a variable in the calling
procedure, not by assigning a new value to the formal parameter name
(changing the binding), but by invoking setitem on the shared datum
(altering the bound datum itself).
The following chart is a graphic representation of the ideas in the
last paragraph. The three columns represent Pascal call by value, Pascal
call by reference, and Logo. In each case the main program has two arrays
named actual and other; it then invokes a procedure proc
using actual as the actual argument providing the value for
proc's formal parameter formal. Here are the programs:
| Pascal call by value | Pascal call by reference | |
|---|---|---|
program pgm;
type pair = array [0..1]
of integer;
var actual,other: pair;
procedure proc(formal:pair);
begin
body
end
begin
actual[0] := 3;
actual[1] := 4;
other[0] := 5;
other[1] := 6;
proc(actual)
end.
| program pgm;
type pair = array [0..1]
of integer;
var actual,other: pair;
procedure proc(var formal:pair);
begin
body
end
begin
actual[0] := 3;
actual[1] := 4;
other[0] := 5;
other[1] := 6;
proc(actual)
end.
|
| Logo |
|---|
make "actual {3 4}@0
make "other {5 6}@0
proc :actual
to proc :formal
body
end
|
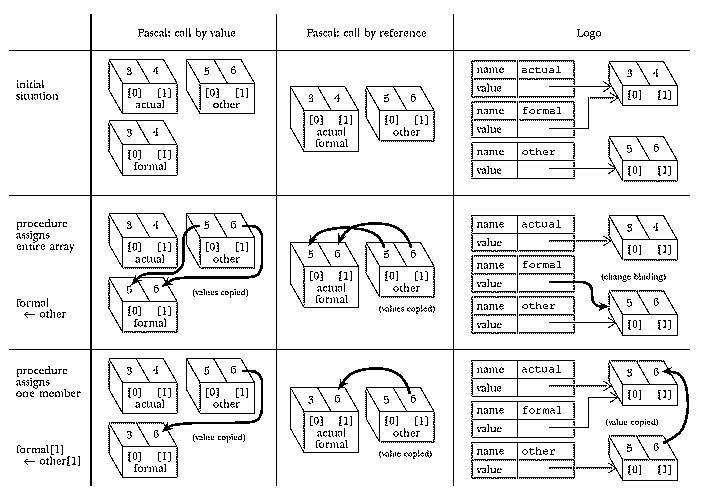
The first row of the figure shows the situation when proc is
entered, before its body is executed. The second row shows what happens if
proc contains an assignment of other to formal, i.e.,
formal := other
in either Pascal version or
make "formal :other
in the Logo version. The third row shows what happens if, instead,
proc contains an assignment of just one member of the array, i.e.,
formal[1] := other[1]
in either Pascal version or
setitem 1 :formal (item 1 :other)
in the Logo version. Your goal is to see what happens to
actual in each case when proc is finished.
Our final Pascal program example, showing the use of call by reference, is a version of the partition sort from Chapter 3 that uses the technique of exchanging two array members when appropriate to divide the array into two partitions "in place" (without requiring the allocation of extra arrays to hold the partitions). This program is adapted from Jon Bentley's version in Programming Pearls (Addison-Wesley, 1986). It's much closer in style to the real quicksort than my list-based version.
In the partition sort program of Chapter 3, I had to put a lot of effort into preventing a situation in which every member of the list being sorted ended up on the same side of the partition value. The quicksort solution starts by choosing some member of the array as the partition value and excluding that member from the partitioning process. As a result, the worst possible case is that the n members of the array are divided into the partitioning member, a partition of size n−1, and a partition of size zero. If we're unlucky enough to hit that case every time, we'll have an O(n2) running time, but not an infinite loop.
How do we choose the partitioning member? It turns out that just picking one at random is surprisingly successful; sometimes you get a very bad choice, but usually not. But in this program I'm using a popular method that tends to work a little better (that is, to give more balanced partition sizes): The program finds the first member of the unsorted array, the last member, and the one halfway in between, and chooses the median of these three values--the one that's neither the largest nor the smallest.
Once the partitioning member has been chosen, the goal is to rearrange the array members into an order like this:

If other members of the array have the same value as the one we've chosen as the partitioning member, it doesn't really matter in which partition they end up. What does matter is that before doing the partitioning, we don't know where in the array the partitioning member will belong, so how can we keep from bumping into it as we rearrange the other members? The solution is that the partitioning member is temporarily kept in the leftmost possible position; the other members are partitioned, and then the partitioning member is swapped back into its proper position.
The partition works using two index variables i and j,
which start at the leftmost and rightmost ends of the part of the array that
we're sorting. (Remember that this algorithm uses recursive calls to sort
each partition, so that might not be all 100 members of the full array.) We
move i toward the right, and j toward the left, until we find
two members out of place. That is, we look for a situation in which
data[i] is greater than the partitioning member and data[j] is
smaller than the partitioning member. We then interchange those two members
of the array and continue until i and j meet in the middle.
Procedure exch has two variable parameters and exchanges their values.
Program psort illustrates a fairly common but not obvious technique:
the array data contains 100 "real" members in positions 0 to 99 but
also has a "fence" or "sentinel" member (with index 100)
just so that the program doesn't have to make a special case check for the
index variable i reaching the end of the array. The
value of data[100] is guaranteed to be greater than all the numbers that
are actually being sorted. Having this extra member in the array avoids the
need for an extra comparison of the form
if i > upper then ...
and thereby helps make the program a little faster.
program psort;
{partition sort demo}
var data: array [0..100] of integer;
i: integer;
procedure showdata;
{print the array}
var i: integer;
begin {showdata}
for i := 0 to 99 do
begin
if i mod 20 = 0 then writeln;
write(data[i]:3)
end;
writeln;
writeln
end; {showdata}
function median(lower,upper:integer):integer;
{find the median of three values from the data array}
var mid: integer;
begin
mid := (lower+upper) div 2;
if (data[lower] <= data[mid]) and (data[mid] <= data[upper]) then
median := mid
else if (data[lower] >= data[mid]) and
(data[mid] >= data[upper]) then
median := mid
else if (data[mid] <= data[lower]) and
(data[lower] <= data[upper]) then
median := lower
else if (data[mid] >= data[lower]) and
(data[lower] >= data[upper]) then
median := lower
else median := upper
end;
procedure sort(lower,upper:integer);
{sort part of the array}
var key,i,j:integer;
procedure exch(var a,b:integer);
{exchange two integers}
var temp:integer;
begin {exch}
temp := a;
a := b;
b := temp
end; {exch}
begin {sort}
if upper > lower then
begin
exch (data[lower],data[median(lower,upper)]);
key := data[lower];
i := lower;
j := upper+1;
repeat
i := i+1
until data[i] >= key;
repeat
j := j-1
until data[j] <= key;
while (i <= j) do
begin
exch(data[i], data[j]);
repeat
i := i+1
until data[i] >= key;
repeat
j := j-1
until data[j] <= key
end;
exch(data[lower], data[j]);
sort(lower,j-1);
sort(i,upper)
end
end; {sort}
begin {main program}
data[100] := 200;
for i := 0 to 99 do
data[i] := random(100);
writeln('Data before sorting:');
showdata;
sort(0,99);
writeln('Data after sorting:');
showdata
end.
Brian Harvey,
bh@cs.berkeley.edu