1996-09 Solution
 A proof by induction:
A proof by induction:
- Base Case #1: n = 0 means a 1x1 chessboard. Removing that one tile
leaves nothing left to be tiled, so we've tiled the chessboard with 0 tiles.
- Base Case #2: n = 1 means a 2x2 chessboard. Removing that one tile
leaves exactly a triomino, which we put down at the proper orientation.
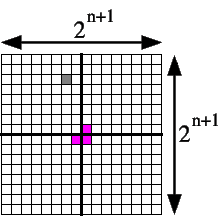
- Induction step: We assume we can tile a 2n by 2n
chessboard with a square removed from it. To tile the 2n+1 by
2n+1 chessboard with a square removed from it, we divide the
chessboard down the middle horizontally and vertically. This cuts the chessboard
into 4 equal 2n by 2n blocks. The missing square
will be in one of those sections, WLOG let's say it's in the upper-left
section. We know from induction that we can tile that section. The remaining
three sections are tiled by removing the square closest to the center from
each of these 2n by 2n sections. These 3 sections
with that square removed can be tiled by induction. The central three squares
removed (shown in magenta below) perfectly form a triomino, so we use one
additional triomino to fill that region, and we're done.
WWW Maven: Dan
Garcia (ddgarcia@cs.berkeley.edu)
 Send me feedback
Send me feedback




 A proof by induction:
A proof by induction:  A proof by induction:
A proof by induction: