[temperature, pressure, humidity, wind velocity(3)] =
Weather (longitude,latitude,elevation,time)
The state is thus a 6-tuple of continuous variables, each of
which depends on 4 continuous parameters. The governing equations
are partial differential equations (PDEs), which describes
how each of the 6 variables changes as a function of all the others.
Other, simpler examples include
d u(x,t) (u(x-h,t)-u(x,t))/h - (u(x,t)-u(x+h,t))/h
-------- = C * -----------------------------------------
dt h
where C is a constant of proportionality. For small h,
u(x-h,t)-u(x,t) d u( x - h/2, t)
--------------- ~ - ----------------
h dt
and
u(x,t)-u(x+h,t) d u( x + h/2, t)
--------------- ~ - ----------------
h dt
and so
(u(x-h,t)-u(x,t))/h - (u(x,t)-u(x+h,t))/h d^2 u(x,t)
----------------------------------------- ~ ----------
h d x^2
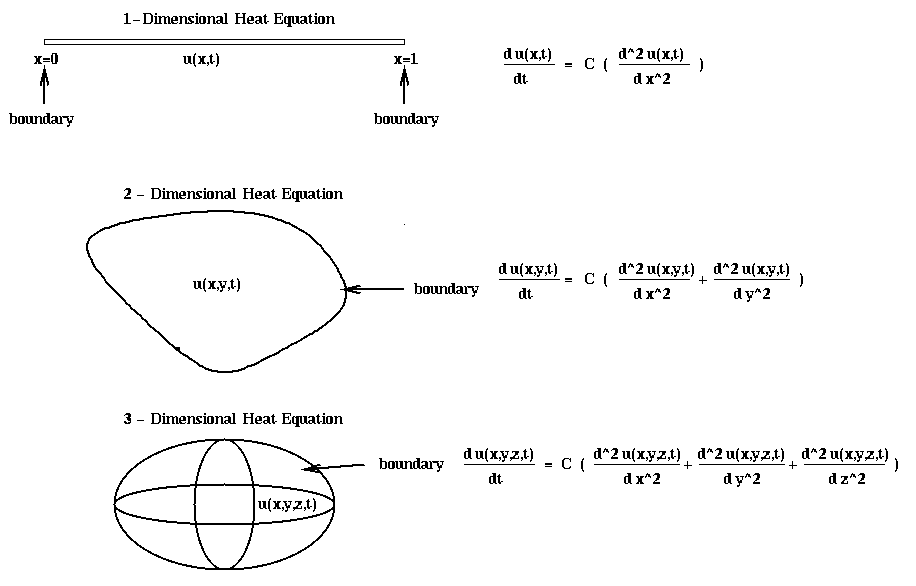
Thus in the limit as h --> 0, we get the heat equation
d u(x,t) d^2 u(x,t)
-------- = C * ----------
dt d x^2
C is called the conductivity of the bar. To solve this equation,
we still need the boundary conditions, or the temperatures
at the ends of the bar (u(0,t) and u(1,t) for all t >= 0),
and the initial conditions, or the temperature of the bar at time t=0
(u(x,0) for all 0 <= x <= 1).
If instead of a 1-dimensional bar, we have a 2-dimensional plate of some shape, the heat equation becomes
d u(x,y,t) d^2 u(x,y,t) d^2 u(x,y,t)
---------- = C * ( ------------ + ------------ )
dt d x^2 d y^2
= C * 2D-Laplacian(u)
with boundary conditions consisting of temperature specified all along the
1-dimensional boundary of the plate, and the initial conditions consisting of
the temperature at every point in the plate at t=0.
Finally, if we have a complete 3-dimensional object, the heat equation becomes
d u(x,y,z,t) d^2 u(x,y,z,t) d^2 u(x,y,z,t) d^2 u(x,y,z,t)
------------ = C * ( -------------- + -------------- + -------------- )
dt d x^2 d y^2 d z^2
= C * 3D-Laplacian(u)
with boundary conditions consisting of temperature all along the 2-dimensional
boundary of the body, and initial conditions consisting of the temperature
throughout the body at t=0. (Note that the Laplacian is defined both
for functions of 2 and of 3 variables.)

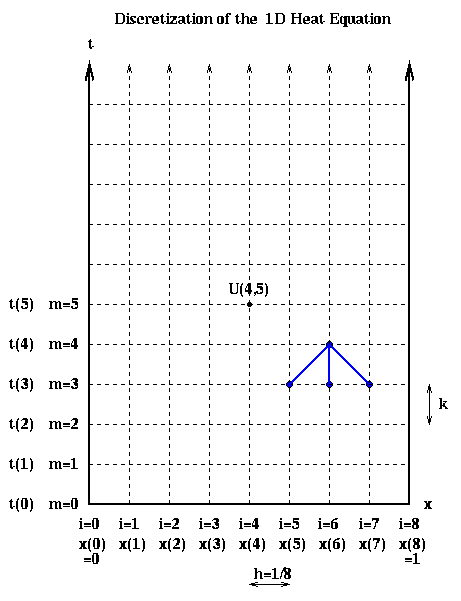
The initial condition u(x,0) tells us the value of U(i,0) at all the grid points along the bottom row in the figure, the boundary condition u(0,t) tells us the value of U(0,m) at the all grid points along the left boundary of the figure, and the boundary condition u(1.0,t) tells us the value of U(n,m) at all the grid points along the right boundary of the figure.
Having discretized the state variable u(x,t), the initial condition, and the boundary conditions, we need to discretize the governing equation. There are a variety of ways to do this. The simplest way is analogous to the forward Euler method we described in the last lecture. We approximate du(x(i)-h/2,t(m))/dx and du(x(i)+h/2,t(m))/dx by the finite differences
d u( x(i)-h/2, t(m) ) u( x(i), t(m) ) - u( x(i)-h, t(m) ) U(i,m)-U(i-1,m)
--------------------- ~ ----------------------------------- ~ ---------------
dx h h
and
d u( x(i)+h/2, t(m) ) u( x(i)+h, t(m) ) - u( x(i), t(m) ) U(i+1,m)-U(i,m)
--------------------- ~ ----------------------------------- ~ ---------------
dx h h
and then d^2 u(x(i),t(m))/ dx^2 by the finite difference
d^2 u(x(i),t(m)) d u( x(i)+h/2, t(m) )/dx - d u( x(i)-h/2, t(m) )/dx
---------------- ~ -----------------------------------------------------
d^2 x h
u(x(i-1),t(m)) - 2*u(x(i),t(m)) + u(x(i+1),t(m))
~ ------------------------------------------------
h^2
U(i-1,m) -2*U(i,m) + U(i+1,m)
~ -----------------------------
h^2
We then approximate d u(x,t)/dt by
d u(x(i),t(m)) u(x(i),t(m+1)) - u(x(i),t(m)) U(i,m+1) - U(i,m)
-------------- ~ ----------------------------- ~ -----------------
d t k k
Combining the last two expressions yields the equation
U(i,m+1) - U(i,m) U(i-1,m) - 2*U(i,m) + U(i+1,m)
----------------- = ------------------------------
k h^2
To use this as an algorithm, we assume we know the temperature u for all x(i)
at time t(m), and solve the equation for the temperature for all x(i) at
the next time step t(m+1)=t(m)+k:
k
U(i,m+1) = U(i,m) + ( --- ) * ( U(i-1,m) - 2*U(i,m) + U(i+1,m) )
h^2
= z * U(i-1,m) + (1-2*z) * U(i,m) + z * U(i+1,m)
where z = k/h^2 is a constant. In terms of the last figure, this gives us a
formula to compute the values of U(i,m+1) at all the internal grid points in
row m+1 of the discretization, in terms of the values of U(m,i) in row m.
Explicit solution of the 1D Heat Equation
for m = 1 to final m
for i = 1 to n-1
U(i,m+1) = z * U(i-1,m) + (1-2*z) * U(i,m) + z * U(i+1,m)
end for
end for
The algorithm is called explicit because it uses an explicit formula
for the value of U(i,m+1) in terms of old data.
Note that U(i,m+1) depends on exactly three values in the row below it.
This pattern is indicated in blue in the discretization above, and is called
the stencil of the algorithm.
Parallelism is available in this problem by dividing the mesh on the bar up into contiguous pieces, and assigning them to different processors, with processors responsible for updating the values at the mesh points they own. This is shown in the figure below for 4 processors. Since the boundary points require no computation, the leftmost and rightmost processors have 1 fewer grid point to update. Because the stencil only requires data from grid points to the immediate left and right, only data at the boundary of the processors needs to be communicated. Thus, the parallelism shares the surface-to-volume effect with our parallelization of particle systems, because most work is in internal to the data owned by a processor, and only data on the boundary needs to be communicated.

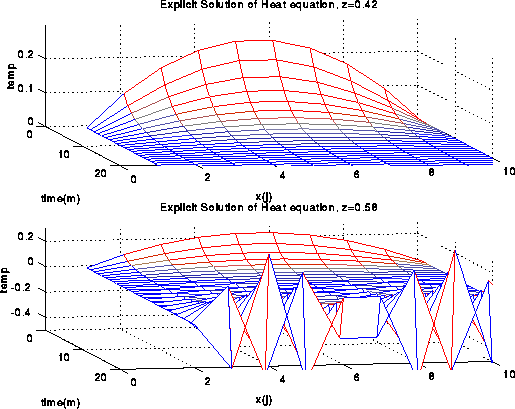
This is very simple to parallelize and indeed efficiency is very good for large numbers of mesh points. However, much as Euler's method kept us from taking large time steps when we solved certain ODEs, the same happens here. In fact it is easy to see that unless we keep z <= .5, or k <= .5*h^2, the solution becomes unstable and oscillates wildly, taking on values arbitrarily large and small, in great contrast to the correct physical solution. (See Supplementary Notes on the Stability of the Explicit Solution of 1D Heat Equation for a proof.) An example is shown in the figure below, where the temperature of the bar is held to 0 at the boundaries, and initially, at time t=0, the bar is warm (red) in the middle and cold (blue) near the boundaries. As time progresses, the bar should cool off and the temperature approach zero throughout. This is indeed computed by Euler's method when z = .42 (the top graph), but not when z = .58 (the bottom figure).
u(x(i),t(m+1)) - u(x(i),t(m))
----------------------------- ~
k
1 u(x(i-1),t(m)) - 2*u(x(i),t(m)) + u(x(i+1),t(m))
- * ( -----------------------------------------------------
2 h^2
u(x(i-1),t(m+1)) - 2*u(x(i),t(m+1)) + u(x(i+1),t(m+1))
+ ------------------------------------------------------)
h^2
leading to the formula
U(i,m+1) - U(i,m)
----------------- =
k
1 U(i-1,m) - 2*U(i,m) + U(i+1,m)
- * ( -----------------------------------
2 h^2
U(i-1,m+1) - 2*U(i,m+1) + U(i+1,m+1)
+ ------------------------------------ )
h^2
Solving for U(*,m+1) yields
-z/2 * U(i-1,m+1) + (1+z) * U(i,m+1) - z/2 * U(i+1,m+1) =
z/2 * U(i-1,m) + (1-z) * U(i,m) + z/2 * U(i+1,m)
where as before z=k/h^2. This may also be written as
a tridiagonal linear system of equations
[ 1+z -z/2 ] [ U(1,m+1) ]
[ -z/2 1+z -z/2 ] [ U(2,m+1) ]
[ ... ] [ ... ]
[ -z/2 1+z -z/2 ] * [ U(i,m+1) ] =
[ ... ] [ ... ]
[ -z/2 1+z -z/2 ] [ U(n-2,m+1) ]
[ -z/2 1+z ] [ U(n-1,m+1) ]
[ (1-z) * U(1,m) + z/2 * U(2,m) ]
[ z/2 * U(1,m) + (1-z) * U(2,m) + z/2 * U(3,m) ]
[ ... ]
[ z/2 * U(i-1,m) + (1-z) * U(i,m) + z/2 * U(i+1,m) ]
[ ... ]
[ z/2 * U(n-3,m) + (1-z) * U(n-2,m) + z/2 * U(n-1,m) ]
[ z/2 * U(n-2,m) + (1-z) * U(n-1,m) ]
where for simplicity we have used the boundary conditions U(0,:) = U(n,:) = 0.
We may abbreviate this linear system as
( I + (z/2)*T) * U(:,m+1) = b(m) = ( I - (z/2)*T) * U(:,m)
where T is the tridiagonal matrix
[ 2 -1 ]
[ -1 2 -1 ]
T = [ ... ]
[ -1 2 -1 ]
[ -1 2 ]
This leads to the overall algorithm
Implicit solution of the 1D Heat Equation -- Crank-Nicholson
for m = 1 to final m
b(m) = ( I - (z/2)*T) * U(:,m)
Solve ( I+(z/2)*T)*U(:,m+1) = b(m) for U(:,m+1)
end for
(For a proof that the solution remains bounded no matter how large
a time step we take,
see
Supplementary Notes on
the Stability of the Implicit Solution of 1D Heat Equation
.)
The algorithm is called implicit because it requires the solution of a
linear system to compute U(:,m+1), so that each U(i,m+1) depends on U(k,m)
for all k. On a serial machine this linear system
may be solved in O(n) operations using
Gaussian elimination, about the same as the explicit method. This is because
there is no fill-in outside the three nonzero diagonals during Gaussian
elimination. On a parallel machine, however, parallelism is harder to come by
than before. The entries of b(m) may be computed in parallel using the same
stencil operation as the explicit algorithm, but solving the linear system
is harder. We might be tempted to try parallel-prefix
(see Lecture 10)
but this is of no use when we move to the more interesting higher dimensional
case.
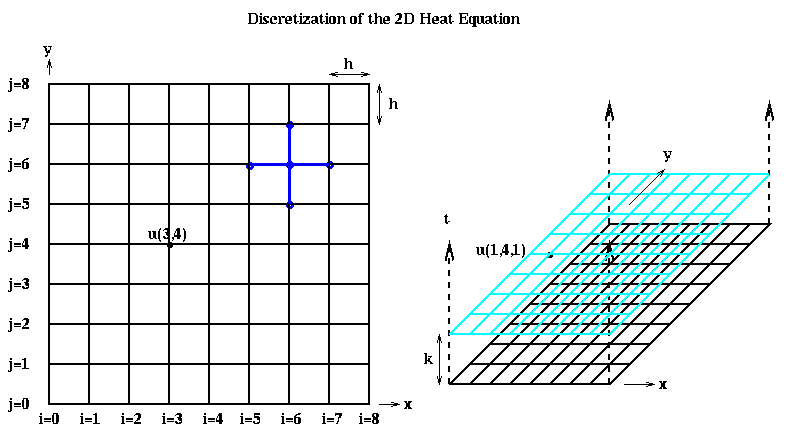
We approximate the two second-derivatives of u with respect to x and y similarly as before:
d^2 u(x(i),y(j),t(m))
---------------------
d x^2
u(x(i-1),y(j),t(m)) - 2*u(x(i),y(j),t(m)) + u(x(i+1),y(j),t(m))
~ ---------------------------------------------------------------
h^2
U(i-1,j,m) - 2*U(i,j,m) + U(i+1,j,m)
~ ------------------------------------
h^2
and
d^2 u(x(i),y(j),t(m))
---------------------
d y^2
u(x(i),y(j-1),t(m)) - 2*u(x(i),y(j),t(m)) + u(x(i),y(j+1),t(m))
~ ---------------------------------------------------------------
h^2
U(i,j-1,m) - 2*U(i,j,m) + U(i,j+1,m)
= ------------------------------------
h^2
so summing the last two terms
U(i-1,j) + U(i+1,j) + U(i,j-1) + U(i,j+1) - 4*U(i,j)
2D-Laplacian(U)(i,j) ~ ----------------------------------------------------
h^2
= Discrete-2D-Laplacian(U)(i,j)
As with the 1D Heat Equation, we can use either the explicit Euler algorithm:
U(i,j,m+1) - U(i,j,m)
--------------------- = Discrete-2D-Laplacian(U)(i,j)
k
which is equivalent to
U(i,j,m+1) = U(i,j,m) + k*Discrete-2D-Laplacian(U)(i,j,m)
k
= (1 - 4*---) * U(i,j,m) +
h^2
k
---*(U(i-1,j,m) + U(i+1,j,m) + U(i,j-1,m) + U(i,j+1,m))
h^2
or the implicit Crank-Nicholson algorithm:
U(i,j,m+1) - U(i,j,m) 1
--------------------- = - * ( Discrete-2D-Laplacian(U)(i,j,m+1) +
k 2
Discrete-2D-Laplacian(U)(i,j,m) )
which is equivalent to
k
U(i,j,m+1) - - * Discrete-2D-Laplacian(U)(i,j,m+1) =
2
k
U(i,j,m) + - * Discrete-2D-Laplacian(U)(i,j,m)
2
or
k k
(1 + 2*---) * U(i,j,m+1) - ----- * ( U(i-1,j,m+1) + U(i+1,j,m+1) +
h^2 2*h^2
U(i,j-1,m+1) + U(i,j+1,m+1) )
k k
= (1 - 2*---) * U(i,j,m) + ----- * ( U(i-1,j,m) + U(i+1,j,m) +
h^2 2*h^2
U(i,j-1,m) + U(i,j+1,m) )
= b(i,j,m)
As before, implementing Euler's method involves setting each U(i,j,m+1) to a
weighted average of its north, south, east and west neighbors on a grid;
this stencil is shown in blue above and below.
Parallelization involves assigning
subsets of grid points to processors, as shown below.
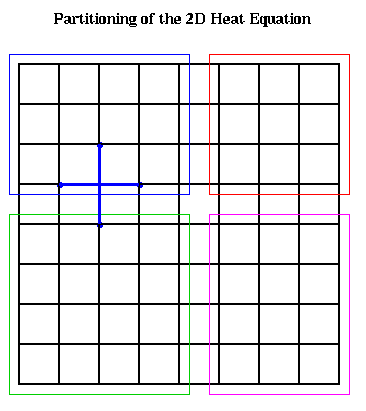
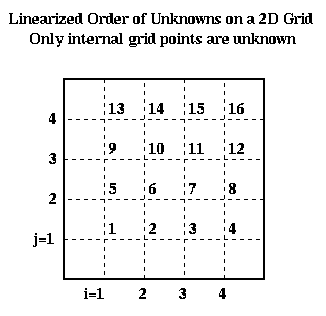
Implementing Crank-Nicholson requires solving a system of linear equations. Let us show what this matrix looks like. To write down this matrix, we need to make a linear list of the unknowns U(i,j,m+1), so we can put them in a vector. We illustrate below:
For simplicity, let a = 1+2*k/h^2 and c = -k/(2*h^2). This lets us write the linear system as H*U=b, or

More generally, we get an (n-1)^2-by-(n-1)^2 block-tridiagonal matrix, with blocks that are (n-1)-by-(n-1). The diagonal blocks are identical tridiagonal matrices with a on the diagonal and c on the offdiagonals. The offdiagonal blocks are all c times the (n-1)-by-(n-1) identity matrix.
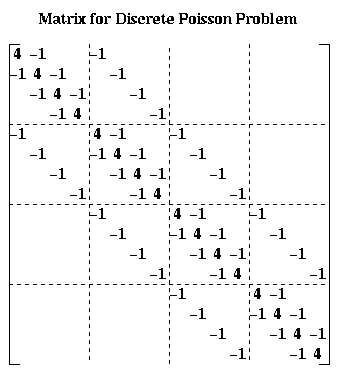
This special case is called the discrete Poisson equation. We call the above matrix H in the discussion below. See the section on electrostatic force and gravity below to see where this case arises. Given these values of a and c, we have chosen the number of iterations so the solution provides about as accurate a solution to the underlying continuous heat equation as the direct methods (i.e. taking the discretization error into account).
Algorithm Type Serial Time PRAM Time Storage #Procs
--------- ---- ----------- --------- ------- ------
Dense LU D N^3 N N^2 N^2
Band LU D N^2 N N^(3/2) N
Jacobi I N^2 N N N
Inv(H)*b D N^2 log N N^2 N^2
CG I N^(3/2) N^(1/2)*log N N N
SOR I N^(3/2) N^(1/2) N N
Sparse LU D N^(3/2) N^(1/2) N*log N N
FFT D N*log N log N N N
Multigrid I N (log N)^2 N N
Lower Bound N log N N
Key to abbreviations:
Dense LU: Gaussian elimination, treating H as dense
Band LU : Gaussian elimination, treating H as zero outside a band
of half-width n-1 near diagonal
Sparse LU : Gaussian elimination, exploiting entire
zero-structure of H
Inv(H)*b : precompute and store inverse of H, multiply it by
right-hand-side b
CG : Conjugate Gradient method
SOR : Successive Overrelaxation
FFT : Fast Fourier Transform based method
There are several interesting features of this table. The Lower Bound is the time required to compute any N numbers which are themselves nontrivial functions of N other numbers. Note that this lower bound is actually attained (in the O(.) sense) both in the serial and parallel cases, but by different algorithms. Multigrid is the fastest serial algorithm, and the FFT is second fastest. In the PRAM model, they trade places, and the FFT is fastest. Later we will study both algorithms, which use divide-and-conquer but in quite different ways: parallelizing the FFT requires fast matrix transposes, and Multigrid requires operating on a quadtree. In particular, we will do more realistic performance modeling, incorporating communication time, in order to see which one is faster in practice.
We include a variety of other algorithms, not because they are competitive for the discrete Poisson equation, but because they are more widely applicable than to the discrete Poisson equation. Dense LU (Gaussian elimination) is discussed at length in other lectures. Band LU is similar, but avoids storage and arithmetic outside the bandwidth of size sqrt(N)=n-1. Both result in filling in many of the zero entries in the coefficient matrix. Sparse LU exploits the entire zero structure of H (and its L and U factors) to avoid all storage of and arithmetic with 0 entries. It will be discussed in another lecture.
The method inv(H)*b means that we precompute and store the explicit inverse of H once and for all; this is not counted as part of the computational cost, but just storage. Then solving a linear system H*x=b requires multiplying b by the explicit inverse, at a cost of 2n^2 serial flops. This method is impractical because of the enormous storage required, and is not even as fast as the most rudimentary iterative method, Jacobi.
Jacobi's method is an iterative solver, and at each iteration replaces the current approximate solution at (i,j) by a weighted average of its nearest neighbors on the grid; its stencil is the same as for Euler. It therefore is parallelized much like the explicit Euler solver. SOR (Successive Overrelaxation) uses a more clever weighted average than Jacobi, and also only updates the grid points in two phases. It converges much more quickly. Jacobi and SOR work best on matrices, like H, that are diagonally dominant, i.e. where the diagonal is sufficiently larger than the offdiagonals.
CG (Conjugate Gradients) applies to any linear system system like H*x=b, where H is a symmetric matrix as well as positive definite. Such matrices are very common in engineering practice. (Three equivalent definitions of positive definiteness are that (1) all of H's eigenvalues must be positive; (2) x'*H*x > 0 for all nonzero vectors x; and (3) there must be an LU factorization of the form H = L*L'.) The computational bottleneck of CG is a matrix-vector multiplication by H, and so effective parallelization requires grid partitioning as described earlier.
In addition to the methods in this table being in increasing order of speed for solving Poisson's equation, they are (roughly) in order of increasing specialization, in the sense that Dense LU can be used in principle to solve any linear system, whereas the FFT and Multigrid only work on equations quite similar to Poisson's equation. In practice, one wants the fastest method suitable for one's problem, and it often takes a great deal of specialized knowledge to make this decision. Fortunately, on-line help is available to help make this decision at the "templates" subdirectory of Netlib, especially the on-line book "Templates for the Solution of Linear Systems".
-(x,y,z)/r^3
where r = sqrt(x^2 + y^2 + z^2). Instead of dealing with the force,
which is a vector, it is easier to deal with a potential
V(x,y,z), which is the scalar
V(x,y,z) = -1 / r
One can easily confirm that the force is just the negative of the
gradient of the potential
d V(x,y,z) d V(x,y,z) d V(x,y,z)
- grad V(x,y,z) = - ( ---------- , ---------- , ---------- )
dx dy dz
The intuition behind the potential is that V is the height of a hill at a point (x,y,z), and the corresponding force just pushes a particle at (x,y,z) downhill, in the direction of steepest descent (the direction in which V decreases most rapidly). This is shown below in 2D.
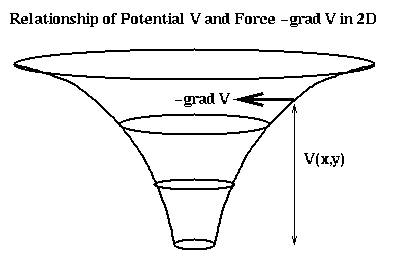
It is straightforward to confirm that V(x,y,z) satisfies
3D-Laplacian(V) = 0
except at r=0, where V has a singularity. The above equation
is called Laplace's equation. When masses or charged particles
are present (the more interesting case), then we instead get
Poisson's equation
3D-Laplacian(V) = f
where f describes the density of mass or of charge. Combined with
appropriate boundary conditions (like the value of V along a square
boundary), these equations can be solved by discretizing the
same way as in the last section. Thus, we may solve for electrostatic
or gravitational force by first computing the potential V by solving
Poisson's equation numerically, and then computing the gradient of
V numerically.
For simplicity we often consider gravity or electrostatic forces in the plane, by which we mean the solution of the 2D problem
2D-Laplacian(V) = f
This is not a real physical potential, but captures mathematically
many of the properties of the real problem, and since it is 2D and
so cheaper to solve than the 3D problem, it is widely used.
Discretizing it using the same finite difference approach as
above yields the discrete Poisson equation H*v=f, where
v is a vector of unknowns, f is given and H is the discrete Poisson
matrix described in the last section.