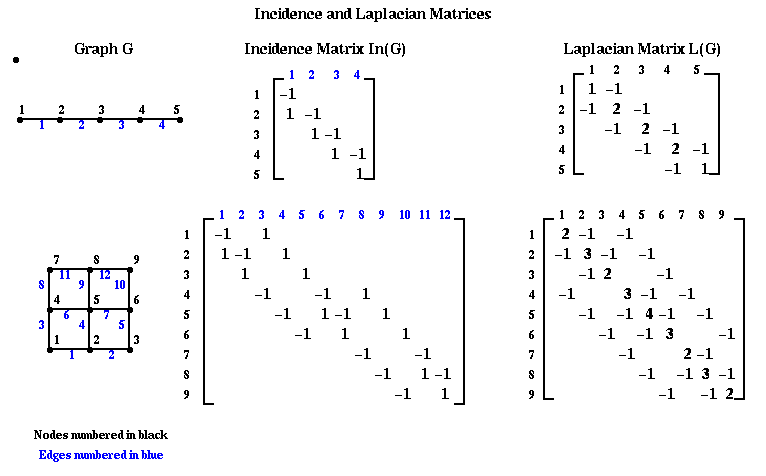
We will first describe the algorithm, and then give three related justifications for its efficacy. Let G=(N,E) be an undirected, unweighted graph without self edges (i,i) or multiple edges from one node to another. We define two matrices related to this graph.
Definition The incidence matrix In(G) of G is an |N|-by-|E| matrix, with one row for each node and one column for each edge. Suppose edge e=(i,j). Then column e of In(G) is zero except for the the i-th and j-th entries, which are +1 and -1, respectively.
Note that there is some ambiguity in this definition, since G is undirected; writing edge e=(i,j) instead of (j,i) is equivalent to multiplying column e of In(G) by -1. We will see that this ambiguity will not be important to us.
Definition The Laplacian matrix L(G) of G is an |N|-by-|N| symmetric matrix, with one row and column for each node. It is defined as follows.
(L(G))(i,j) = degree of node i if i=j
(number of incident edges)
= -1 if i!=j and there is an edge (i,j)
= 0 otherwise
Here are some small examples. Note the similarity between the Laplacian graph of the mesh, and the matrix for the discrete Poisson equation, introduced in Lecture 13. With a zero right hand side, we also called this discrete equation Laplace's equation. We will pursue this physical analogy below.

The following theorem state some important facts about In(G) and L(G). It introduces us to the idea that the eigenvalues and eigenvectors of L(G) are related to the connectivity of G.
Theorem 1. Given a graph G, its associated matrices In(G) and L(G) have the following properties.
norm(In(G)'*v)2
lambda = ------------------
norm(v)2
where norm(z)2 = sumi z(i)2
= sum{all edges e=(i,j)} (v(i)-v(j))2
----------------------------------
sumi v(i)2
For a proof of this theorem, click here.
Part 6 of Theorem 1 motivates the following definition.
Definition (M. Fiedler, "Algebraic Connectivity of Graphs", Czech. Math. J. 23:298--305, 1973). lambda2(L(G)) is called the algebraic connectivity of G.
Now we can state our algorithm for spectral bisection of a graph.
Compute the eigenvector v2
corresponding to lambda2 of L(G)
for each node n of G
if v2(n) < 0
put node n in partition N-
else
put node n in partition N+
endif
endfor
First we show that this partition is at least reasonable, because it tends to give connected components N- and N+:
Theorem 2. (M. Fiedler, "A property of eigenvectors of nonnegative symmetric matrices and its application to graph theory", Czech. Math. J. 25:619--637, 1975.) Let G be connected, and N- and N+ be defined by the above algorithm. Then N- is connected. If no v2(n) = 0, N+ is also connected.
For a partial proof, click here.
There are a number of reasons lambda2 is called the algebraic connectivity. Here is another.
Theorem 3. (Fiedler). Let G=(N,E) be a graph, and G1=(N,E1) a subgraph, i.e. with the same nodes and a subset of the edges, so that G1 is "less connected" than G. Then lambda2(L(G1)) <= lambda2(L(G)), i.e. the algebraic connectivity of G1 is also less than or equal to the algebraic connectivity of G.
We will prove this later, after we introduce more machinery.
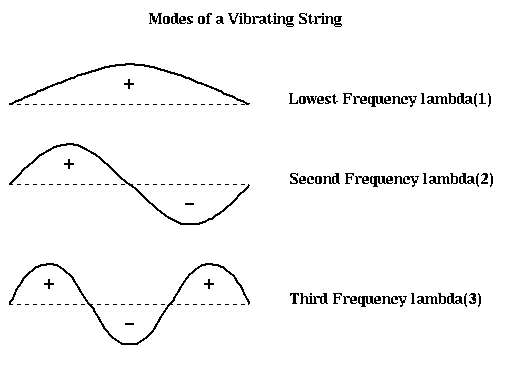
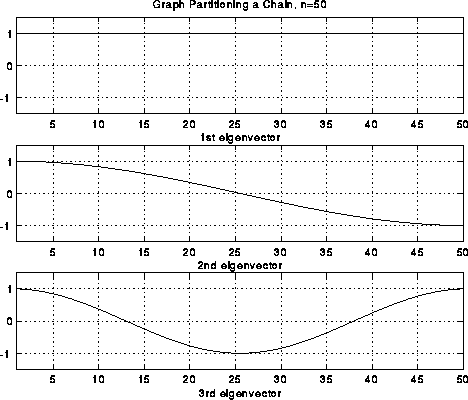
Note that we have also labeled each part of the string as to whether it is above the rest position (+), or below (-). In the case of the second frequency lambda2, half the string is labeled +, and half is labeled -, effectively bisecting the string into two equal sized, connected components. It turns out that if we build this vibrating string from a finite set of identical masses (nodes) connected by identical springs (edges), write down Newton's Laws of motion for the masses, and solve for the frequencies and shapes of the vibrational modes, we will get precisely the eigenvalues and eigenvectors of the Laplacian L(G) of the graph G, where G consists of a chain of nodes with nearest neighbor connections. Therefore, the second eigenvector of L(G) is the shape of the second mode of vibration, and divides the graph in half.
In the case of more complicated graphs than simple chains, the same intuition applies. It is easiest to understand in the case of planar graphs, which we can think of as a kind of trampoline; again the second mode of vibration divides the graph (trampoline) into two halves.
Let us perform this construction more explicitly in the case of a string. In the figure below, we let x(i) represent the (small) displacement of mass i from the horizontal.
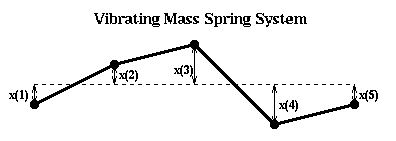
If the displacement is small, the force on mass i is
force(i) = k*(x(i-1)-x(i)) + k(x(i+1)-x(i))
= k*(x(i-1) - 2*x(i) + x(i+1))
where k is a spring constant. We assume that the spring from x(i) to x(i+1) is stretched
proportional to the distance x(i+1)-x(i). If this difference is positive, so mass i+1 is
higher than mass i, then the force is upwards, or positive. Newton's law tells us F=ma or
d2 x(i)
m * -------- = force(i)
d t2
= k*(x(i-1) - 2*x(i) + x(i+1))
We need to be careful about what happens at the end masses. The simplest, and nearly correct,
decision is to fix x(0)=x(n+1)=0 (like a taut spring). This lets us write down the system of ODEs
[ x(1) ] [ 2*x(1)-x(2) ]
m * d2 [ x(2) ] [ -x(1)+2*x(2)-x(3) ]
------ [ .... ] = -k * [ ... ]
d t2 [ x(n-1)] [ -x(n-2)+2*x(n-1)-x(n) ]
[ x(n) ] [ -x(n-1)+2*x(n) ]
[ 2 -1 ] [ x(1) ]
[ -1 2 -1 ] [ x(2) ]
= -k * [ ... ] * [ .... ]
[ -1 2 -1 ] [ x(n-1)]
[ -1 2 ] [ x(n) ]
[ x(1) ]
[ x(2) ]
= -k * M * [ .... ]
[ x(n-1)]
[ x(n) ]
or yet more briefly,
d2 x(t)
-(m/k) * -------- = M * x(t)
d2 t
where x(t) is a vector [x(1),...,x(n)]'. We seek solutions of the form
x(t) = sin(a*t)*x0, where a and x0 are a scalar and vector to be determined. Plugging in to the
last equation yields
(m/k)*a2*sin(a*t)*x0 = M * sin(a*t) * x0
Canceling sin(a*t), which is (almost always) zero, yields
M * x0 = (m/k)*a2 * x0 = e * x0
Thus x0 is an eigenvector of M and e=(-m/k)*a2 is an eigenvalue. We know the eigenvalues and
eigenvector of M explicitly; as can be confirmed by simple trigonometry, the i-th pair is given by
[ sin(1*i*pi/(n+1)) ]
[ sin(2*i*pi/(n+1)) ]
x0 = [ ...... ]
[ sin((n-1)*i*pi/(n+1)) ]
[ sin(n*i*pi/(n+1)) ]
e = 2*(1-cos(i*pi/(n+1)))
In other words, we just get sine curves of varying frequencies, exactly matching the curves
pictured above. Furthermore, when n is large and i is small,
(m/k) * a2 = e
= 2*(1-cos(i*pi/(n+1)))
~ ( i*pi/(n+1) )2
so the frequency of vibration
a ~ sqrt(k/m)*pi/(n+1) * i
In other words, the frequencies of successive modes of vibrations are just multiples of
the base frequency, thus providing the harmonics we expect from a plucked string.
Unfortunately, M is not quite the Laplacian L(G) of the simple graph G of n nodes connected in a chain; the (1,1) and (n,n) entries are 2 instead of 1. To make the analogy between spectral bisection and the vibrating string exact, we need a slightly different mass-spring system. This is shown in the figure below. There are n horizontal rods, and on each rod a mass m can slide back and forth frictionlessly. These identical masses are connected with identical springs as before. x(i) is the horizontal displacement from rest.
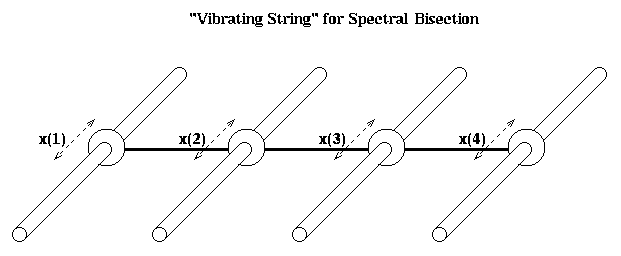
The only difference from before in the equations of motion is for masses 1 and n, the ones at the end. Since they are only tied to one moving mass, rather than one moving mass and one fixed endpoint, we get
d2 x(1)
m * -------- = force(1) = k*(x(2) - x(1))
d t2
and
d2 x(n)
m * -------- = force(1) = k*(x(n-1) - x(n))
d t2
which leads to
[ x(1) ] [ x(1)-x(2) ]
m * d2 [ x(2) ] [ -x(1)+2*x(2)-x(3) ]
------ [ .... ] = -k * [ ... ]
d t2 [ x(n-1)] [ -x(n-2)+2*x(n-1)-x(n) ]
[ x(n) ] [ -x(n-1)+x(n) ]
[ 1 -1 ] [ x(1) ]
[ -1 2 -1 ] [ x(2) ]
= -k * [ ... ] * [ .... ]
[ -1 2 -1 ] [ x(n-1)]
[ -1 1 ] [ x(n) ]
[ x(1) ]
[ x(2) ]
= -k * L(G) * [ .... ]
[ x(n-1)]
[ x(n) ]
One can again confirm by simple trigonometry, that the i-th eigenvalue and eigenvector of L(G) are
given by
[ cos((0+.5) *(i-1)*pi/n) ]
[ cos((1+.5) *(i-1)*pi/n) ]
x0 = [ ...... ]
[ cos((n-1.5)*(i-1)*pi/n) ]
[ cos((n-.5) *(i-1)*pi/n) ]
e = 2*(1-cos((i-1)*pi/n))
which are just simple cosine curves, the fist few of which are pictured below. Again, the second
eigenvector effectively divides the nodes in half.
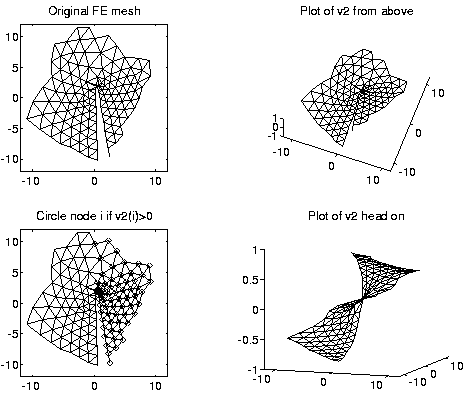
The same analogy applies to other graphs. For example, here is the same approach applied to a planar graph, which is a simple model of a plate with a crack in it. Physically, one expects the line along the crack to be the weak point, and lead to the second lowest frequency of vibration as the object flexes along the crack, and the second eigenvector picks this out.
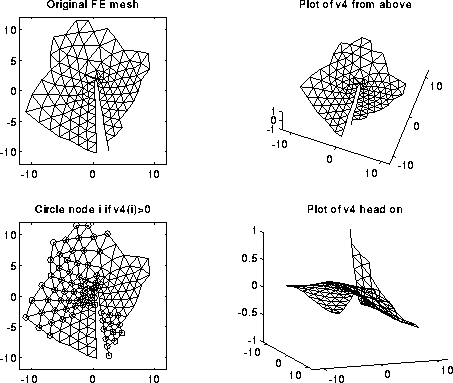
From the above pictures, one might also expect higher order eigenvectors to be able to partition a graph into even more parts at a time than 2. This is borne out by examing the 4th eigenvector of the cracked plate, show below. Indeed, many of the results we discuss extend to higher eigenvectors, but we limit our discussion to the second eigenvector, which is most widely used in practice.
Lemma 1. Let G=(N,E) be a graph, and N = N- U N+ be an arbitrary disjoint partitioning of N. Define a column vector x, with x(i) = +1 if i is in N+, and x(i) = -1 if i is in N-. Let L(G) be the Laplacian of G. Then
# edges connecting N+ and N-
= .25 * x' * L(G) * x
= .25 * sumi,j x(i) * L(G)(i,j) * x(j)
This may also be written
# edges connecting N+ and N-
= .25 * sum{all edges e=(i,j)} (x(i) - x(j))2
Proof of Lemma 1.
x' * L(G) * x
= sumi,j L(G)(i,j)*x(i)*x(j)
= sumi=j L(G)(i,i)*x(i)2 +
sumi!=j L(G)(i,j)*x(i)*x(j)
= sumi=j L(G)(i,i)
+ sum{i!=j, i, j both in N+ } L(G)(i,j)*x(i)*x(j)
+ sum{i!=j, i, j both in N- } L(G)(i,j)*x(i)*x(j)
+ sum{i!=j, i, j in N- and N+ } L(G)(i,j)*x(i)*x(j)
= sumi degree(i)
+ sum{i!=j, i, j both in N+ } (-1)*(+1)*(+1)
+ sum{i!=j, i, j both in N- } (-1)*(-1)*(-1)
+ sum{i!=j, i, j in N- and N+ } (-1)*(+1)*(-1)
= 2 * ( #edges in G )
- 2*( #edges connecting nodes in N+ to nodes in N+ )
- 2*( #edges connecting nodes in N- to nodes in N- )
+ 2*( #edges connecting nodes in N- to nodes in N+ )
= 4 * ( #edges connecting nodes in N- to nodes in N+ )
To prove the second expression in the lemma, use part 3 of Theorem 1 to note that
x' * L(G) * x = x' * In(G) * (In(G))' * x
= sum{edges e=(i,j)} ( (In(G))' * x)e )2
= sum{edges e=(i,j)} (x(i) - x(j))2
This completes the proof. QED
Lemma 1 lets us restate the graph partitioning problem as finding N+ and N-, i.e. a vector x whose entries are +1 or -1, so that
minimum #edges in a partition of N =
min{x(i) = +1 or -1, sumi x(i) = 0} .25*x'*L(G)*x
We will replace this discrete problem by a simpler continuous problem, by minimizing
over a larger set of x's than just +-1 vectors, namely all vectors x such that sumi x(i)2 = |N|.
In other words, we will compute the z minimizing
min{sumi z(i)2 = |N|, sumi z(i) = 0} .25*z'*L(G)*z
Given z, we will "round it" by computing x(i) = sign(z(i)) to get an assignment.
To see how this is connected to eigenvalues of L(G), we state without proof the following result from linear algebra, which is a special case of the Courant Fischer Minimax Theorem (R. Horn and C. Johnson, "Matrix Analysis", 1988).
Theorem 4. If A is a symmetric matrix with eigenvalues lambda1 <= lambda2 <= ... and eigenvectors v1, v2, ..., then
lambda2 = min{v != 0, v'*v1 = 0} v'*A*v / v'v
and the minimizing v is v2.
For a proof of this special case, click here.
To apply this to graph partitioning, recall that lambda1 = 0 and v1 = [1,...,1]', so the condition v'*v1=0 is the same as sumi v(i) = 0. Substituting v = z/sqrt(|N|) above yields
min{sumi z(i)2 = |N|, sumi z(i) = 0} .25*z'*L(G)*z
= min{sumi v(i)2 = 1, sumi v(i) = 0} .25*|N|*v'*L(G)*v
.25*|N|*v'*L(G)*v
= min{sumi v(i)2 = 1, sumi v(i) = 0} -----------------
v'*v
since v'*v = sumi v(i)2 = 1
= .25 * |N| *
v'*L(G)*v
min{sumi v(i)2 = 1, v'*v1 = 0} ---------
v'*v
= .25 * |N| * lambda2
We have nearly proven
Theorem 5. The minimum # edges connecting N+ and N- in any partitioning of G=(N,E) into equal parts N = N+ U N-, is at least .25 * |N| * lambda2.
So the larger the "algebraic connectivity" lambda2, the more edges we need to cut to separate the graph.
Proof of Theorem 5. The minimum number of edges is
min{x(i) = +1 or -1, sumi x(i) = 0} .25*x'*L(G)*x
>= min{sumi x(i)2 = |N|, sumi x(i) = 0} .25*x'*L(G)*x
since we are minimizing over
a larger set of vectors x
= .25 * |N| * lambda2
QED
In the case of a chain of n nodes, we stated earlier that lambda2 = 2*(1-cos(pi/n)) ~ (pi/n)2 so the lower bound in Theorem 5 is about .25 * pi2 / n, which is low by a factor of n. For an d-dimensional grid with nd nodes, it turns out lambda2 is exactly d times as large as lambda2 for a chain, and again the lower bound of Theorem 5 is about n times too low (O(nd-2) instead of nd-1). For a star graph (n-1 nodes all connected to a single, n-th node) or a complete graph (all nodes connected to all other nodes), the lower bound is nearly exact.
Now we return to the proof of Theorem 3. It is easy using part 3 of Theorem 1 and Theorem 4. Let G be a graph, and G1 a subgraph with the same nodes but a subset of the edges. Let G2 be another subgraph with the same nodes and the complementary set of edges. Let In(G1) and In(G2) be the incidence matrices of G1 and G2, respectively. It is easy to see that In(G) = [ In(G1) , In(G2) ], if we number the edges in G1 before the edges in G2. Therefore, by part 3 of Theorem 1,
L(G) = In(G) * (In(G))'
= [ In(G1) , In(G2) ] * [ In(G1) , In(G2) ]'
= In(G1) * (In(G1))' + In(G2) * (In(G2))'
= L(G1) + L(G2)
Thus, by Theorem 4,
lambda2(G)
= min{v != 0, sumi v(i) = 0} v'*L(G)*v / v'*v
= min{v != 0, sumi v(i) = 0} v'*(L(G1)+L(G2))*v / v'*v
>= min{v != 0, sumi v(i) = 0} v'* L(G1) *v / v'*v
+ min{v != 0, sumi v(i) = 0} v'* L(G2) *v / v'*v
since we are minimizing over
a larger set of vectors
= lambda2(G1) + lambda2(G2)
>= lambda2(G1)
This completes the proof of Theorem 3.
The algorithm of choice for this problem is Lanczos. Given any n-by-n sparse symmetric matrix A, Lanczos computes a k-by-k symmetric tridiagonal matrix T, whose eigenvalues are good approximations of the eigenvalues of T, and whose eigenvectors can be used to get approximate eigenvectors of A. Building T requires k matrix-vector multiplications with A; this is typically the most expensive part of the algorithm. One hopes to get a good enough approximation with k much small than n. This means one only approximates a small subset of k of A's n eigenvalues. Fortunately, the ones which converge first are the largest and the smallest, including lambda2.
There are many variations on Lanczos. We present the simplest possible version below, and refer the reader to the literature for details. See, for example, "The Symmetric Eigenvalue Problem", B. Parlett, Prentice Hall, 1980. You may also see on-line help page for Lanczos, which is experimental and is likely to move in the future.
Choose an arbitrary starting vector r
b(0) = norm(r) = sqrt( sumi r(i)2 )
i = 0
repeat
i = i+1
v(i) = r / b(i-1)
r = A * v(i) ... matrix-vector multiply,
... the most expensive step
r = r - b(i-1)*v(i-1) ... "saxpy", costs 2n flops
a(i) = v(i)' * r ... dot-product, costs 2n flops
r = r - a(i)*v(i) ... "saxpy", costs 2n flops
b(i) = norm(r)
until convergence ... details omitted
At each step i, the algorithm computes a tridiagonal matrix
[ a(1) b(1) ]
[ b(1) a(2) b(2) ]
T = [ b(2) a(3) b(3) ]
[ ... ]
[ b(i-2) a(i-1) b(i-1) ]
[ b(i-1) a(i) ]
whose eigenvalues approximate the eigenvalues of A. Let w(2) be the second eigenvector of T.
Then the corresponding approximate eigenvector of A is
sumj=1,...,i w(2)(j) * v(j)
The reader may already have noticed an irony of using this algorithm to compute v2. One of the major motivations of graph partitioning was to accelerate matrix-vector multiplication by a symmetric matrix M. We are proposing to form the graph G(M), then its Laplacian L(G(M)), and then multiply by L(G(M)) repeatedly in the Lanczos algorithm. But M and L(G(M)) have the same pattern of nonzero entries, so multiplying by L(G(M)) is as hard as multiplying by M. Therefore, spectral partitioning via Lanczos is of use only when one expects to multiply by M many more times than by L(G(M)).
To summarize, we may use divide-and-conquer to partition G0 = (N0,E0) as follows: G=(N,E) as follows:
( N+, N- ) = Recursive_partition( N, E )
... recursive partitioning routine returns N+ and N-
... where N = N+ U N-
If |N| is small
Partition G=( N, E ) directly to get N = N+ U N-
Return ( N+, N- )
else
(1) Compute a coarse approximation Gc = ( Nc, Ec )
(2) ( Nc+ , Nc- ) = Recursive_partition( Nc, Ec )
(3) Expand ( Nc+, Nc- ) to a partition ( N+, N- )
(4) Improve the partition ( N+, N- )
Return ( N+, N- )
endif
Steps (1), (3) and (4) in the above algorithm require further explanation. We describe two approaches to implementing these steps. The first approach is described in ``A fast and high quality multilevel scheme for partitioning irregular graphs'', by G. Karypis and V. Kumar; a software package implementing this method (among others) is called METIS. A similar algorithm is available in Chaco, and described in A multilevel algorithm for partitioning graphs, B. Hendrickson and R. Leland, Proc. Supercomputing '95.
The second approach is described in "A fast multilevel implementation of recursive spectral bisection for partitioning unstructured problems" by Barnard and Simon, Proceedings of the 6th SIAM Conference on Parallel Processing for Scientific Computing, 1993.
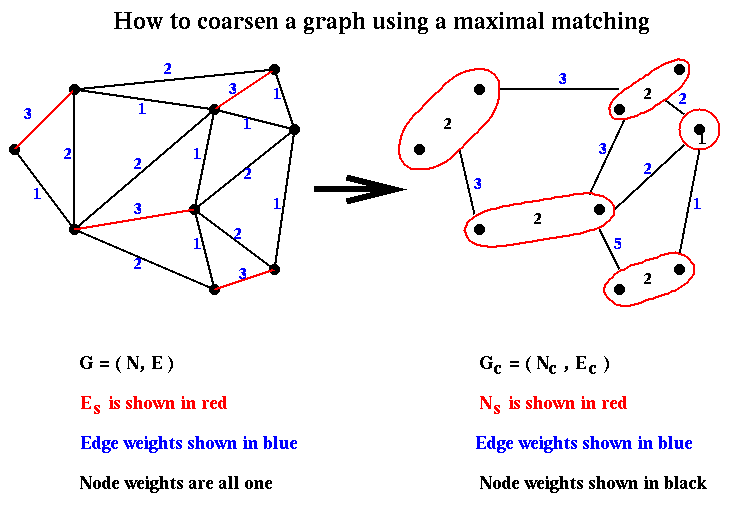
Gc is computed in step (1) of Recursive_partition as follows. We define a matching of a graph G=(N,E) as a subset Em of the edges E with the property that no two edges in Em share an endpoint. A maximal matching is one to which no more edges can be added and remain a matching. We can compute a maximal matching by a simple random algorithm:
let Em be empty
mark all nodes in N as unmatched
for i = 1 to |N| ... visit the nodes in a random order
if node i has not been matched,
choose an edge e=(i,j) where j is also unmatched,
and add it to Em
mark i and j as matched
end if
end for
Given a matching, Gc is computed as follows. We let there be
a node r in Nc for each edge in Em. Then we
construct Ec as follows:
for r = 1 to |Em| ... for each node in Nc
let (i,j) be the edge in Em corresponding to node r
for each other edge e=(i,k) in E incident on i
let ek be the edge in Em incident on k, and
let rk be the corresponding node in Nc
add the edge (r,rk) to Ec
end for
for each other edge e=(j,k) in E incident on j
let ek be the edge in Em incident on k, and
let rk be the corresponding node in Nc
add the edge (r,rk) to Ec
end for
end for
if there are multiple edges between pairs of nodes of
Nc, collapse them into single edges
Note that we can take node weights
into account by letting the weight of a node (i,j) in Nc be the sum of
the weights of the nodes i and j. We can similarly take edge weights into account
by letting the weight of an edge in Ec be the sum of the weights of
the edges "collapsed" into it. Furthermore, we can choose the edge (i,j) which
matches j to i in the construction of Nc above to have the
large weight of all edges incident on i; this will tend to minimize the weights
of the cut edges. This is called heavy edge matching in
METIS,
and is illustrated below.
Given a partition (Nc+,Nc-) from step (2) of Recursive_partition, it is easily expanded to a partition (N+,N-) in step (3) by associating with each node in Nc+ or Nc- the nodes of N that comprise it. This is again shown below:
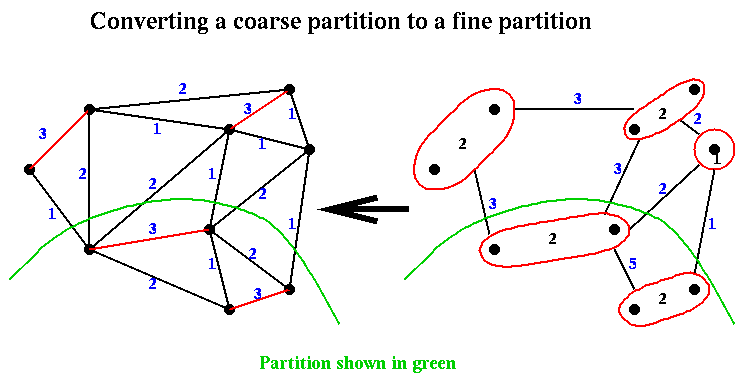
Finally, in step (4) of Recurive_partition, the approximate partition from step (3) is improved using a variation of Kernighan-Lin.
Now we turn to the divide-and-conquer algorithm of Barnard and Simon, which is based on spectral partitioning rather than Kernighan-Lin. The expensive part of spectral bisection is finding the eigenvector v2, which requires a possibly large number of matrix-vector multiplications with the Laplacian matrix L(G) of the graph G. The divide-and-conquer approach of Recursive_partition will dramatically decrease the cost.
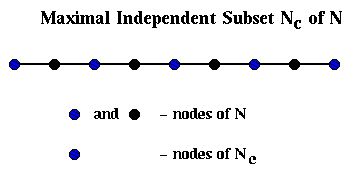
Barnard and Simon perform step (1) of Recursive_partition, computing Gc = (Nc,Ec) from G=(N,E), slightly differently than above: They find a maximal independent subset Nc of N. This means that
Nc = empty set
for i = 1 to |N|
if node i is not adjacent to any node already in Nc
add i to Nc
end if
end for
This is shown below in the case where G is simply a chain of 9 nodes with
nearest neighbor connections, in which case Nc consists simply of every
other node of N.
To build Ec, we proceed as follows: We will loop through the edges in E, growing "domains" Di around each node i in Nc. In other words, a domain consists of the subgraph of G connected to i by the edges examined so far. We will add an edge to Ec whenever an edge in E would connect two of these domains.
Ec = empty set
for all nodes i in Nc
Di = ( { i }, empty set ) ... build initial domains
end for
unmark all edges in E
repeat
choose an unmarked edge e=(i,j) from E
if exactly one of i and j (say i) is in some Dk
mark e
add j and e to Dk
else if i and j are in different Dks (say Dki and Dkj)
mark e
add an edge (ki,kj) to Ec
else if both i and j are in the same Dk
mark e
add it to Dk
else
leave e unmarked
endif
until no unmarked edges
For example, suppose we start with G being a chain of nodes as above, with nodes and edges numbered from left to right. Then domain Di for node i will just contain its neighbor to the right, and the edges in Ec will simply connect adjacent nodes in Nc, so Gc is just the chain of length n/2.
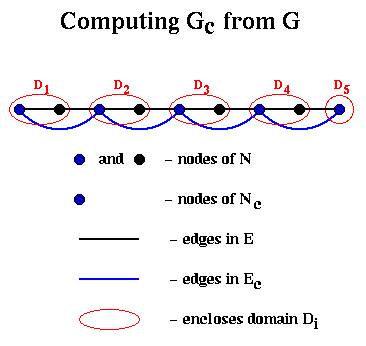
This completes the discussion of Barnard and Simon's implementation of step (1) of Recurive_partition.
Here is how Barnard and Simon implement step (3). Recall that the partitioning is done by using the signs of the components of the second eigenvector of the Laplacian. Assuming that we have computed an approximate second eigenvector v2 (Gc) of Gc, we must compute an approximate second eigenvector v2 (G) of G. This is done by interpolation:
for each node i in N
if i is also a node in Nc, then
v2(G)(i) = v2(G1)(i),
... i.e. use the same eigenvector component
else
v2(G)(i) = average of v2(G1)(j)
for all neighbors j of i in Nc.
end if
end for
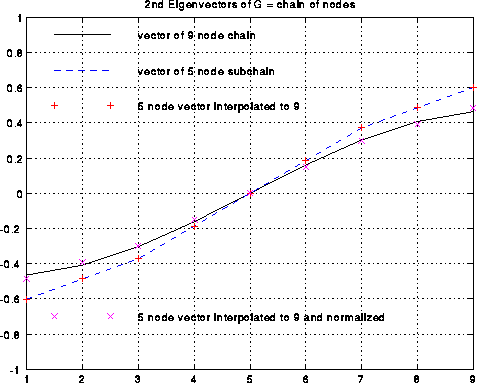
This is shown below in the case of the chain of 9 nodes. The black line
is the exact v2(G) (normalized so the sum-of-squares is one).
The dashed blue line is the exact v2(Gc), also normalized, and
which only connects every other node.
The red +'s are the approximate v2(G) computed by interpolation as
above, which by construction lie on top of the blue line.
The magenta x's are the red +'s normalized, to better see how well they
approximate the black line.
Step (4) of Recursive_partition involves refining this approximate second eigenvector to be more accurate. Refining the approximate second eigenvector can be done in several ways. (The unrefined approximate second eigenvector is not always as good as in the case of the chain!). One possibility is that the Lanczos algorithm mentioned above benefits from having a starting vector which mostly points in the direction of the desired eigenvector. More aggressively, one can use a technique called Rayleight Quotient Iteration, which uses the fact that the iteration
choose a starting vector v(0)
... we use v2(Gc)
v(0) = v(0) / norm2(v(0))
... norm2(x) = sqrt(sumi x(i)2)
i=0
repeat
i = i+1
rho(i) = v(i-1)' * L(G) * v(i-1)
... rho(i) = Rayleigh Quotient
v(i) = ( L(G) - rho(i)*I )-1 * v(i-1)
v(i) = v(i) / norm2(v(i))
until convergence
converges asymptotically cubically to an eigenvalue-eigenvector pair
(rho(i),v(i)); this means the the error cubes at every step, so that for example
an error of 10-4 turns into an error of
(10-4)3 = 10-12 after one step.
rho(i) costs one matrix-vector multiply. Computing v(i), i.e.
solving the linear system (L(G) - rho(i)*I) * v(i) = v(i-1), is done using
an iterative method (called SYMMLQ) which requires yet more matrix-vector
multiplications. But since cubic convergence
is so fast, very few steps are needed. This speedy convergence is illustrated
below by the example of the chain, where the black line is the
error in the approximate eigenvector v(i) and the dashed blue line is the
error in the approximate eigenvalue rho(i), as functions of i.
One can see the cubic convergence between iterations i=2 and i=3,
where the eigenvector error goes from 10-4 to 10-12.
Cubic convergence is only visible for this one step before hitting the
accuracy limit of 10-16 due to roundoff.
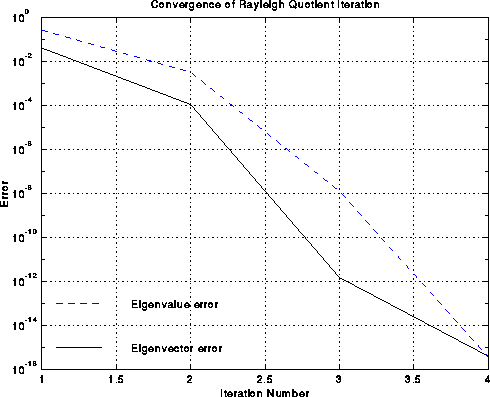
Experiments report a 10x speedup over the basic spectral bisection algorithm.
Recall that there are two classes of algorithms: geometric algorithms, that use coordinate information associated with nodes of the graph, and coordinate-free algorithm, that do not use this information. Accordingly, we present two studies comparing geometric algorithms, as well as coordinate-free ones.
We begin with geometric algorithms. The following data is taken from "Geometric Mesh Partitioning: Implementation and Experiments". Table 1 below describes the 7 graphs being partitioned. All are meshes in 2 or 3 dimensional space, rather than completely general graphs. The first four are 2-dimensional, and the last two are 3 dimensional. The fifth graph, PWT, is sometimes called "two-and-a-half dimensional", because it is a thin ("almost 2D") surface lying in 3D space. The last two columns give the number of vertices and edges in the graphs. The columns labeled "Grading" says how much larger the longest edges in the graph are than the shortest edges. For example, TRIANGLE is a regular tesselation of the place by identical equilateral triangles, so its grading is 1. AIRFOIL2 is similar to the NASA Airfoil we have seen so often, which has some large and some tiny triangles, the largest 1.3e5 times larger than the smallest.
Mesh Description Mesh Type
---- ----------- ---------
TAPIR Cartoon animal 2-D acute triangles
AIRFOIL2 Three-element airfoil 2-D triangles
TRIANGLE Equilateral triangle 2-D triangles/same size
AIRFOIL3 Four-element airfoil 2-D triangles
PWT Pressurized wind tunnel Thin shell in 3-space
BODY Automobile body 3-D volumes and surfaces
WAVE Space around airplane 3-D volumes and surfaces
Mesh Grading Vertices Edges
---- ------- -------- -----
TAPIR 8.5e4 1024 2846
AIRFOIL2 1.3e5 4720 13722
TRIANGLE 1.0e0 5050 14850
AIRFOIL3 3.0e4 15606 45878
PWT 1.3e2 36519 144794
BODY 9.5e2 45087 163734
WAVE 3.9e5 156317 1059331
Table 1: Test problems. "Grading" is the ratio of
longest to shortest edge lengths.
Table 2 below describes the quality of the partitioning into two subgraphs obtained by four algorithms. Quality is measured by the number of edges crossing the partition boundary, where fewer is better. The four algorithms are
Mesh Spectral Inertial Default Best
Partitioning Random Random
Circle Circle
TAPIR 59 55 37 32
AIRFOIL2 117 172 100 93
TRIANGLE 154 142 144 142
AIRFOIL3 174 230 152 148
PWT 362 562 529 499
BODY 456 953 834 768
WAVE 13706 9821 10377 9773
Table 2: Number of edge crossings
for two-way partitions
Finally, we use the partitioning algorithms 7 times recursively in order to partition the graphs into 2^7 = 128 separate partitions, which one would do on a 128-processor machine. Again, the quality of the partitions is largely comparable.
Mesh Spectral Inertial Default
Partitioning Random
Circle
TAPIR 1278 1387 1239
AIRFOIL2 2826 3271 2709
TRIANGLE 2989 2907 2912
AIRFOIL3 4893 6131 4822
PWT 13495 14220 13769
BODY 12077 22497 19905
WAVE 143015 162833 145155
Table 3: Number of edge crossings for 128-way partitions.
Now we consider coordinate-free algorithms more briefly. According to tests done by Kumar and Karypis, their implementation of multilevel Kernighan-Lin and Leland and Hendrickson's implementation provide partitions of quite similar quality, as does a hybrid multilevel method using both spectral partitioning and Kernighan-Lin. However, theirs is usually twice as fast (or more) s Leland and Hendrickson's, and many times faster than spectral partitioning.
Here is a very simple version of the physical mapping problem for DNA. A molecule of DNA is a very long string consisting of a particular sequence of amino acids chosen from a set of four, which may be called A, C, T and G. For example, one might have the sequence ACCTGACTCGAGACTCG, but many millions long. The sequencing problem is to determine this sequence for a given molecule of DNA. Current biochemical technology permits the following algorithm to be used. One can break up this long DNA string into a great many shorter fragments, which can be separated according to their amino acid sequences. The goal is to represent the original DNA as a sequence of these possibly overlapping fragments in some order. Given the sequences making up each fragment, one then knows the sequence making up the original DNA. To extract this representation in terms of fragments, the following experiments are performed. Each fragment F is allowed to bond to the DNA at a point P where the amino acid sequences match. This point is called a probe, and is typically a set of amino acids at one end of the fragment. If the probe is long enough, it will match at a unique point along the DNA. One records this information in a matrix B, which has one row for each fragment and one column for each probe, by putting a 1 at entry (F,P). One can perform the same kind of experiment to see which other fragments bond to fragment F at the same probe P, implying that they overlap. Each such bond between fragment F' and fragment F at probe P is recorded by storing a 1 at location (F',P) of the matrix B. In this way, looping through all the fragments, the matrix B is eventually filled in with ones (and zeros elsewhere), where B(F,P)=1 means that fragment F matches the DNA at probe P. This is shown below, where we have labeled the fragments in sorted order from left to right, and the probes in sorted order from left to right.
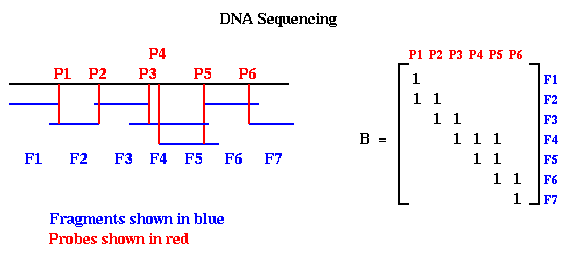
Notice that when the probes and fragments are sorted, B is a band matrix, or more precisely a consecutive-ones matrix, which means that for each row all the ones are consecutive (consecutive-ones matrices are not necessarily band matrices in the usual since, but they often are). In practice, one constructs Bp with probes and fragments in some random order, as shown below. The DNA Sequencing problem is to find the ordering of the rows and ordering of the columns of Bp which expose the underlying band matrix B, because this will say what in what order the fragments appear along the DNA.
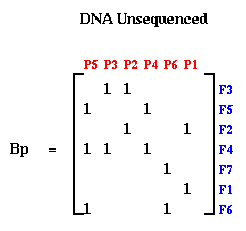
If there were no errors in Bp, this could be done by procedure like breadth first search. But in practice, the laboratory procedure for determining entries of Bp is quite error prone, so we need a method for making Bp "close to" a band matrix in some sense. This is where spectral ordering comes in.
Let G=(N,E) be an undirected graph, and L(G) its Laplacian. Let N = N- U N+ be an arbitrary partition of the nodes, and let x be a column vector, where x(i) = +1 if i is in N+, and x(i) = -1 if i is in N-. In Lemma 1 of the last lecture, we showed that the number of edges connecting N+ and N- was equal to
.25 * sumedges e=(i,j) (x(i) - x(j))2Therefore, the partition N = N- U N+ which minimizes the number of connecting edges is given by the solution x of the minimization problem
min[ x(i) = +1 or -1, sumi x(i) = 0 ]
.25 * sumedges e=(i,j) (x(i) - x(j))2
The spectral partitioning algorithm involved solving the following
approximation:
minsum_i v(i)^2 = |N|, sum_i v(i) = 0
.25 * sumedges e=(i,j) (v(i) - v(j))2
and then choosing x(i) = sign(v(i)).
One can think of this algorithm as embedding the graph G into the real axis, putting node i at location v(i). If e=(i,j) is an edge, then we draw a line segment from v(i) to v(j), which has length |v(i) - v(j)|. The spectral bisection algorithm chooses this embedding into the real axis so as to minimize the sum of squares of the lengths of these line segments, subject to the constraints sum_i v(i)^2 = |N|, and sum_i v(i)=0.
Suppose we start with a symmetric matrix H, form its graph G(H), and apply the above algorithm, yielding a second eigenvector v of L(G(H)). Let P be a permutation matrix, i.e. the identity matrix with its columns permuted, such that the entries of P*v, which are the the entries of v permuted the same way, are in sorted order. Now form K = P*H*P'. K is the matrix H with its rows and columns reordered in the same way that sorts v. The fact that the sum of all (v(i)-v(j))^2 is minimized, means that there are few edges connecting distant v(i) and v(j). In other words, if v(i) and v(j) are widely separated in the sorted list of entries of v, they are unlikely to have an edge connecting them. In the matrix K, this means that there are few nonzero entries far from the diagonal, because these would correspond to an edge from a v(i) to a v(j) widely separated in the sorted list. In other words, K is close to a band matrix.
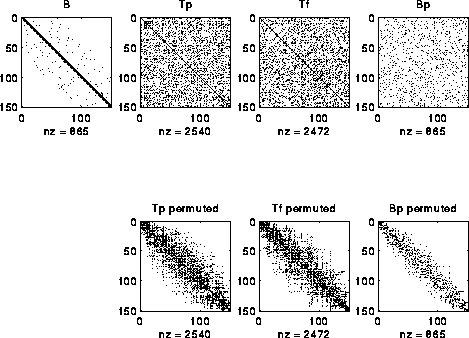
For example, consider the matrix M = L(G), where G is a chain of n nodes. M is a tridiagonal matrix as shown in the figure below. Now perform a random permutation of the rows and columns of M to get H. H has nonzeros uniformly distributed off the diagonal. Apply spectral partitioning to H as described above to get K. As shown below, K is tridiagonal again. (The label nz under each graph is the number of nonzeros entries in the matrix.)
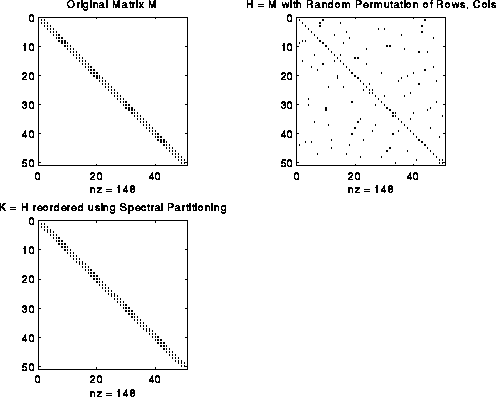
This bandwidth narrowing property (or, more precisely, "consecutive-one-ifying" property) is what we need to reorder the rows and columns of Bp to make it a band (or consecutive-ones) matrix. But reordering Bp requires two permutations, one for the rows and one for the columns, while spectral bisection computes just one permutation. We get around this as follows. We can write Bp = Pf*B*Pp', where Pf and Pp are two unknown permutation matrices we wish to compute; Pf shuffles the rows of B, and Pp shuffles the columns. Now consider the symmetric matrix
Tp = Bp'*Bp = (Pf*B*Pp')'*(Pf*B*Pp') = Pp*(B'*B)*Pp'
Note that Tp only depends on Pp and B, but not on Pf.
If B is a band matrix, one can confirm that B'*B is too, although with
a larger bandwidth. (If B is a consecutive-ones matrix, B'*B shares
a similar property; see
A spectral algorithm for seriation and the consecutive ones problem
for details.)
Thus, Pp can be determined just by using spectral
bisection to find the
single permutation of rows and columns of Tp that makes Pp'*Tp*Pp
(nearly) a band matrix. Similarly one can apply spectral bisection to
Tf = Bp*Bp' = (Pf*B*Pp')*(Pf*B*Pp')' = Pf*(B*B')*Pf'
to independently determine Pf. An example is shown below, where we
start with a perfect band matrix and add a few other random entries to
get B, and randomly permute its rows and columns to get Bp.
The bottom row of three matrices shows Tp, Tf and Bp after permuting
them to make them close to band matrices.
One can see that the construction is far from "perfect", and in fact
degrades more if the random entries added to B are farther from the diagonal.
The physical mapping of DNA remains a hard problem.
The system we will describe is called PARTI, and has more recently been renamed CHAOS. This material is taken from "Distributed Memory Compiler Methods for Irregular Problems -- Data Copy Reuse and Runtime Partitioning," by J. Saltz, R. Das, R. Ponnusamy, and D. Mavripilis, ICASE Report 91-73, NASA Langley Research Center, Hampton VA, 1991.
PARTI is an extension of HPF (High Performance Fortran), and uses the features of HPF for describing array layouts across processors. We begin by reviewing data layouts.
At the end of Lecture 5, we discussed data layout in CM Fortran, where for example the declaration (KEYWORDS are capitalized)
REAL a(64,8), b(64,8), c(64,8)
CMF$ LAYOUT a( :NEWS, :SERIAL ), b( :NEWS, :SERIAL ),
CMF$ LAYOUT c( :SERIAL, :NEWS )
indicated that A(i,j) was to be stored in the j-th memory location of processor
i, the same for B(i,j), and that C(i,j) was instead to be stored in the
i-th memory location of processor j. This would mean that the assignment
A=B could occur in parallel without communication, but that A=C would require
a great deal of communication.
These simple layout directive are not enough for all purposes. In the beginning of Lecture 13, we discussed the more complicated data layouts required to do Gaussian elimination (or other dense linear algebra problems) efficiently on a distributed memory machine, and said the the first four of the following layouts were declarable within the HP Fortran language:

Here, very briefly, is how HPF permits users to declare these kinds of layouts. Rather than saying how each matrix entry maps to a processor location, two levels of indirection are used. The first level declaration declares how many of the available processors are to be used in the layout. A simple example is the following, which declares mygrid to be a linear array of 4 processors.
PROCESSOR mygrid(4)
The second level declares a template, or "virtual array", and
says how to lay it out on mygrid. For example
TEMPLATE template_blocked(100),template_cyclic(100)
DISTRIBUTE template_blocked(BLOCK) ONTO mygrid
DISTRIBUTE template_cyclic(CYLIC) ONTO mygrid
declares that template_blocked(0:24) is mapped to processor 0,
template_blocked(25:49) is mapped to processor 1, and so on,
in general with template_blocked(i) mapping to processor floor(i/25).
Also, template_cyclic(i) is mapped to processor i mod 4.
Block cyclic layouts are also available. Multi-dimensional arrays can
have each subscript mapped independently, as preferred for Gaussian
Elimination.
A template has no memory allocated for it; it just describes a layout. The final level of declaration actually allocates memory for arrays. For example
REAL a(100), b(100), c(100)
ALIGN a(i) WITH template_block(i)
ALIGN b(i) WITH template_block(i)
ALIGN c(i) WITH template_cyclic(i)
declares 3 arrays of 100 entries each. a(i) and b(i) are declared to
be stored at the same place as the template entry template_block(i),
in this case floor(i/25).
However template_block is DISTRIBUTEd, a(i) and b(i)
will always be on the same processor. c(i) is declared to be stored
at the same place as template_cyclic(i), that is i mod 4.
The reason for these levels of indirection is that one can independently control the amount of parallelism (via PROCESSOR), the layout (via DISTRIBUTE) and which variables are local with which other (via ALIGN).
The same mechanism can be used for more irregular layouts, but we need one more level of indirection to specify the irregularity. For example
TEMPLATE irregular(100)
INTEGER map(100)
DATA map/3,2,2,1,1,1,3,0,1,2,... /
... 100 values from 0 to 3
DISTRIBUTE irregular(map) ONTO mygrid
REAL d(100)
ALIGN d(i) WITH irregular(i)
These declarations specify that irregular(i) is mapped to processor map(i),
i.e. irregular(1) is mapped to processor map(1)=3,
irregular(2) is mapped to processor map(2) = 2, and so on.
The ALIGN statement in turn says d(1) is stored on processor 3,
d(2) is stored on processor 2, and so on.
In this example, map is specified at compile-time, and the decision about where to store d(i) is specified at compile-time. This is very limiting, since we probably won't know the actual data structure we need to partition until run-time. The extensions in PARTI to this approach are to allow map to be computed at run time (by examining some user specified loops and doing graph partitioning), and DISTRIBUTE to be executed at run-time as well, in effect recompiling the code at run-time. This is likely to be quite expensive, and so is done only when the user wants to.
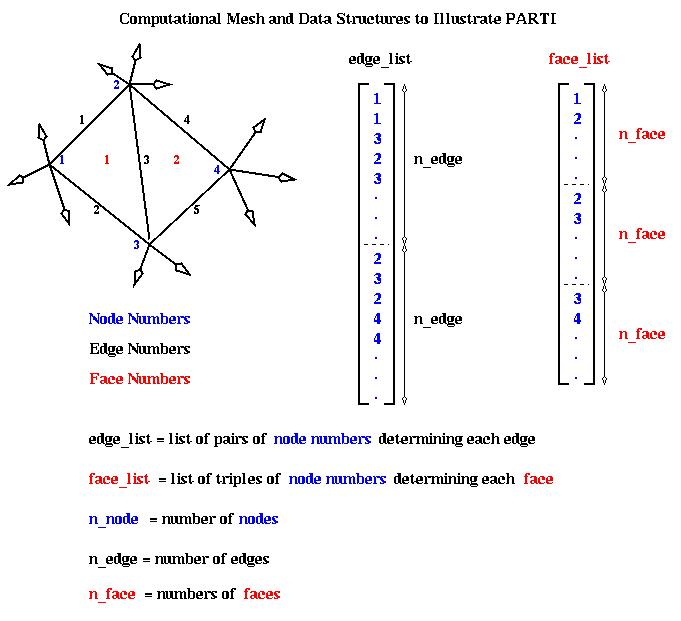
Here is an example, taken from a computational fluid dynamic (CFD) application. The data structure is a two-dimension triangular mesh, made up of nodes (numbered in blue), edges (numbered in black) and faces (numbered in red). The mesh data is stored in two arrays. The edge_list array stores a pair of nodes for each each edge: the nodes numbers for the i-th edge are stored at edge_list(i) and edge_list(i + n_edge), where n_edge is the number of edges. The face_list array stores a triple of nodes for each face: the nodes for the i-th face are stored at face_list(i), face_list(i + n_face), and face_list(i + 2*n_face), as shown below. For example, face 1 has corners at nodes 1, 2 and 3. face 2 at nodes 2, 3 and 4, and so on.
The original sequential program has two data arrays, x and y, which store data associated with each node. In other words x(i) and y(i) are data about the fluid flow at node i. The algorithm has two loops. Loop L1 below loops over all edges, and for each edge updates the data at both nodes determining that edge. Loop L2 loops over all faces, and for each face updates the data at the three nodes determining the face. The functions foo1, foo2, etc, are simple scalar functions of their scalar arguments, whose details do not concern us.
REAL x(n_node), y(n_node)
...
C Loop over all edges
L1: DO i = 1, n_edge
n1 = edge_list(i)
n2 = edge_list(i + n_edge)
y(n1) = foo1(y(n1),y(n2),x(n1),x(n2))
y(n2) = foo2(y(n1),y(n2),x(n1),x(n2))
END DO
C Loop over all faces
L2: DO i = 1, n_face
n1 = face_list(i)
n2 = face_list(i + n_face)
n3 = face_list(i + 2*n_face)
y(n1) = foo4(y(n1),...,x(n3))
y(n2) = foo5(y(n1),...,x(n3))
y(n3) = foo6(y(n1),...,x(n3))
END DO
Here is the parallel version of this program using PARTI:
REAL x(n_node), y(n_node)
TEMPLATE coupling(n_node)
DISTRIBUTE coupling(BLOCK) ONTO mygrid
ALIGN x(i), y(i) WITH coupling(i)
...
C Decide whether to redistribute data
IF (time_to_remap) THEN
DISTRIBUTE coupling(IMPLICIT USING L1)
END IF
C Loop over all edges
IMPLICITMAP(x,y) L1
L1: DO i = 1, n_edge
n1 = edge_list(i)
n2 = edge_list(i + n_edge)
y(n1) = foo1(y(n1),y(n2),x(n1),x(n2))
y(n2) = foo2(y(n1),y(n2),x(n1),x(n2))
END DO
C Loop over all faces
L2: DO i = 1, n_face
n1 = face_list(i)
n2 = face_list(i + n_face)
n3 = face_list(i + 2*n_face)
y(n1) = foo4(y(n1),...,x(n3))
y(n2) = foo5(y(n1),...,x(n3))
y(n3) = foo6(y(n1),...,x(n3))
END DO
Initially, the TEMPLATE coupling is laid out in a blocked fashion onto the processor grid mygrid. Arrays x and y are aligned with coupling. Later, perhaps after the arrays edge_list and face_list have been set up, the user sets time_to_remap to true, and executes the DISTRIBUTE statement following the IF statement. At this point, the system begins the "Inspection phase": It will examine loop L1, which is identified later with the IMPLICITMAP statement. The arguments x and y of IMPLICITMAP tell the system to compute the graph G of data dependencies among the references to x and y in the subsequent loop L1. This is done by executing loop L1 "symbolically", i.e. running through thg loop from i=1 to n_edge, computing the subscripts n1 = edge_list(i) and n2 = edge_list(i + n_edge), seeing that y(n1) depends on y(n1), y(n2), x(n1), and x(n2), and adding nodes n1 and n2, and edge (n1,n2), to graph G, which is initially empty. Functions foo1 and foo2 are not evaluated, and y(n1) and y(n2) are not changed. After computing G, a graph partitioning routine is called to break G into as many pieces as there are processors in mygrid. The partitioning information is stored in the TEMPLATE coupling, with coupling(i) = j if the partition algorithm puts node i onto processor j. All arrays ALIGNed with coupling (namely x and y) are redistributed according to the newly updated coupling. Finally, all parts of the program that reference arrays x or y are "recompiled" to insert the necessary communications to continue to access the data they need.
After completing the "IF (time_to_remap)" block, one reaches loop L1. At this point, the "Execute phase", the newly recompiled code is executed and array y updated. Loop L2 is executed similarly.