
This method shares the quadtree and divide-and-conquer paradigm of Barnes-Hut. It differs in the following ways:
We begin by reviewing the role of the potential, and then return to the FMM.
-(x,y,z)/r3
where r = sqrt(x2 + y2 + z2) is the distance of the particle from the origin.
Instead of dealing with the force, which is a vector, it is often easier to compute the potential phi(x,y,z), which is the scalar
phi(x,y,z) = -1 / r
One can easily confirm that the force is just the negative of the
gradient of the potential
- grad phi(x,y,z) =
d phi(x,y,z) d phi(x,y,z) d phi(x,y,z)
- ( ------------ , ------------ , ------------ )
dx dy dz
The intuition behind the potential is that phi is the height of a hill at a point (x,y,z), and the corresponding force just pushes a particle at (x,y,z) downhill, in the direction of steepest descent (the direction in which phi decreases most rapidly).
Thus, the strategy of the FMM will be to compute a compact expression for the potential phi(x,y,z) which can be easily evaluated, along with its derivative, at any point.
To make the presentation simple, we will do everything in 2D instead of 3D. To motivate the form of the potential we use in 2D, we note that the 3D potential phi(x,y,z) satisfies the 3D Poisson equation
d2 phi(x,y,z) d2 phi(x,y,z) d2 phi(x,y,z)
------------- + ------------- + ------------- = 0
dx2 dy2 dz2
(except at (x,y,z) = 0) as may be easily confirmed. We will analogously
demand that the 2D potential phi(x,y) satisfy the 2D Poisson equation
d2 phi(x,y) d2 phi(x,y)
----------- + ----------- = 0
dx2 dy2
(except at (x,y)=0). The solution for a particle at the origin is
phi(x,y) = log r
so
force = - grad phi(x,y) = -( x, y )/r2
where r = sqrt( x2 + y2 ) is the distance of the particle from the origin.
In other words, we have an inverse-first-power force law instead of an
inverse-square law.
If we have n points in the plane at locations z1, z2, ... , zn (each zi = ( xi, yi )), with masses m1, m2, ... , mn, their potential at a point x will be
phi(x,y) =
sumi=1,...,n mi log sqrt( ( x-xi )2 + ( y-yi )2 )
Our goal is to find a way to evaluate this expression (or its derivative)
at n points, in O(n) time instead of O(n2) time.
r = sqrt( ( x-xi )2 + ( y-yi )2 ) = | z - zi |
Writing z-zi in polar coordinates yields
z - zi = r*esqrt(-1)*theta
= r*cos(theta) + sqrt(-1)*r*sin(theta)
so
log( z - zi ) = log(r) + log(esqrt(-1)*theta )
= log(r) + sqrt(-1)*theta
= log |z-zi| + sqrt(-1)*theta
and
Real( log( z-zi ) ) = log | z-zi |
Thus, the potential is the real part of the complex number
phi(z) = sumi=1,...,n mi * log( z-zi )
This is a differentiable function of the complex variable z (not the case with the absolute value present!), so we can compute its Taylor (or "multipole") expansion. We use the fact that when the |y| < 1, then the Taylor expansion of log( 1-y ) is
log( 1-y ) = y + y2/2 + y3/3 + ...
Thus when |z| is larger than any | zi | we may rewrite phi(z) as
phi(z) = sumi=1,...,n [ mi * log( z-zi ) ]
= sumi=1,...,n [ mi * { log(z) + log( 1 - zi/z ) } ]
= sumi=1,...,n [ mi * log (z) ] +
sumi=1,...,n [ mi * log( 1 - zi/z ) ]
= M * log(z) +
sumi=1,...,n [ mi { sumj=1,...,infinity (zi/z)j / j } ]
... where M = sumi=1,...,n mi
= M * log(z) +
sumj=1,...,infinity [ sumi=1,...,n mi * (zi/z)j / j ]
... reversing the order of summation
= M * log(z) +
sumj=1,...,infinity [ z-j { sumi=1,...,n mi * zij / j } ]
= M * log(z) + sumj=1,...,infinity z-j alphaj
where
alphaj = sumi=1,...,n [ mi * zij / j ]
We "compress" this representation by truncating it, yielding
phi(z) ~ M * log(z) + sumj=1,...,p alphaj / zj
The error in this truncation is proportional to the largest term omitted,
namely
( (max | zi |) / |z| )p+1
For example, if |z| > c * max | zi | with c > 1, then the error is
proportional to 1/cp+1. In particular, suppose all the particles
lie inside a D-by-D square centered at the origin,
so |zi| <= D/sqrt(2). Also suppose that z is outside
a 3*D-by-3*D square centered at the origin, as shown below, so
|z| >= 1.5*D. Then we can take c = (1.5*D)/(D/sqrt(2)) = 3/sqrt(2) ~ 2.12, and so the
error in the formula is O(2.12-p). This fact will let us use a multipole
expansion for the particles in the small box, in any like-sized box
not immediatedly adjacent to it.

If the D-by-D box is centered at zc instead of 0, the idea is similar: We approximate the potential by an expansion around zc:
phi(z) ~ M * log( z-zc ) +
sumj=1,...,p alphaj / ( z-zc )j
If the node in the quadtree corresponding to this box is n, then we
define the data structure representing the multipole expansion associated
with n as
Outer(n) = ( M, alpha1, alpha2, ... , alphap , zc )
For ease of exposition, we will sometimes refer to the expansion associated
with Outer(n) as an outer expansion, since it is to be evaluated
outside n, and to contrast it with the different
expansion discussed in the next section.
sumi=0,...,p betai * ( z-zc )i
This expansion will represent the potential inside the D-by-D box in the
above figure, due to all the particles outside the 3*D-by-3*D box.
We call it an inner expansion, and
represent it by the data structure
Inner(n) = ( beta0, beta1, ... , betap , zc )
The output of the FMM will (partially) consist of Inner(n) for each leaf node n of the quadtree. To explain the algorithm, we need to say how to convert an outer expansion to an inner expansion, and perform related transformations on expansions.
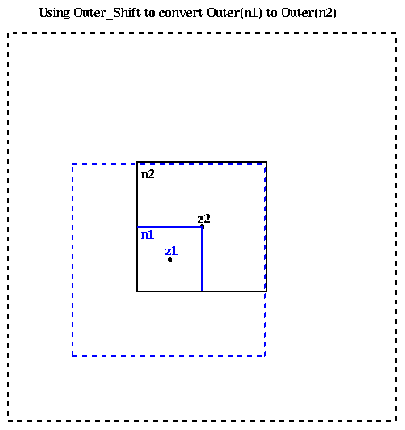
More mathematically, if
Outer( n1 ) = ( M, alpha1,1, alpha1,2, ... , alpha1,p , z1 )
then there is an
Outer( n2 ) = ( M, alpha2,1, alpha2,2, ... , alpha2,p , z2 )
such that for z outside the dashed black box the two outer expansions approximate
each other:
M*log(z- z1 ) + sumi=1,...,p alpha1,i / (z- z1 )i
~ M*log(z- z2 ) + sumi=1,...,p alpha2,i / (z- z2 )i
By doing a little algebra, one can show that
each alpha2,i is a weighted linear sum of all the alpha1,j,
and that the weights are easy to compute; we refer to the
original paper of Greengard and Rokhlin for details.
Thus computing the alpha2,i costs just O(p2).
We refer to this conversion function as
Outer( n2 ) = Outer_shift( Outer( n1 ), center( n2 ) )
where the second argument is the new center for the expansion Outer( n2 ).
We will use Outer_shift in the algorithm to compute Outer(n) for each node in the quad tree by combining the outer expansions of its children.
Inner( n2 ) = ( beta2,0, beta2,1, ... , beta2,p , z2 )for the potential inside n2 due to all the particles outside the dashed black box. Then this expansion also works inside n1 , since n1 is inside n2 . What we want is an expansion Inner( n1 ), centered at z1:
Inner( n1 ) = ( beta1,0, beta1,1, ... , beta1,p , z1 )which gives the potential inside n1 due to the same set of all points outside the dashed black box:
sumi=0,...,p beta1,i * ( z-z1 )i
= sumi=0,...,p beta2,i * ( z-z2 )i
Our job, then, is to take z2 and the beta2,i and compute the beta1,i.
As above, this is a matter of computing certain weighted linear sums of
the beta2,i, and costs O(p2). We denote this transformation by
Inner( n1 ) = Inner_shift( Inner( n2 ), center( n1 ) )
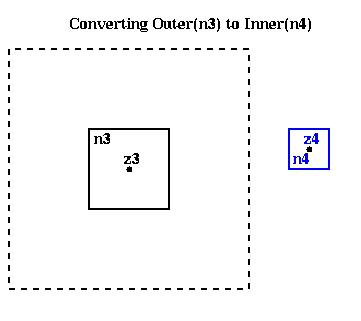
In other words, given
Outer( n3 ) = ( M, alpha3,1, alpha3,2, ... , alpha3,p , z3 )we want to compute an
Inner( n4 ) = ( beta4,1, beta4,2, ... , beta4,p , z4 )
such that
M * log( z-z3 ) + sumi=1,...,p alpha3,i / ( z-z3 )i
~ sumi=0,...,p beta4,i * ( z- z4 )i
Once again, each beta4,i is a weighted sum of all the alpha3,i, so it
costs O(p2) to compute
Inner(n4) = Convert( Outer(n3), center(n4) )
(1) Build the quadtree containing all the points.
(2) Traverse the quadtree from bottom to top,
computing Outer(n) for each square n in the tree.
(3) Traverse the quadtree from top to bottom,
computing Inner(n) for each square in the tree.
(4) For each leaf, add the contributions of nearest
neighbors and particles in the leaf to Inner(n)
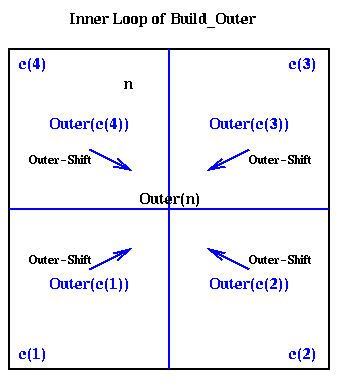
procedure Build_Outer(n)
if n is a leaf
compute Outer(n) using its definition as a sum
else
Outer(n) = 0
for all children c(i) of n ... at most 4 children
Build_Outer( c(i) )
Outer(n) = Outer(n) +
Outer_Shift( Outer( c(i) ), center(n) )
end for
endif
This is shown graphically below, where the outer expansions of the
children c(i) are combined to get the outer expansion of the parent n.
We need only "add" the outer expansions in the sense of adding the
masses M (since the total mass of the particles in n is the sum of the
masses of its children), and adding the coefficients alphai (since the
potential of a collection of particles is the sum of the potentials
of each particle).
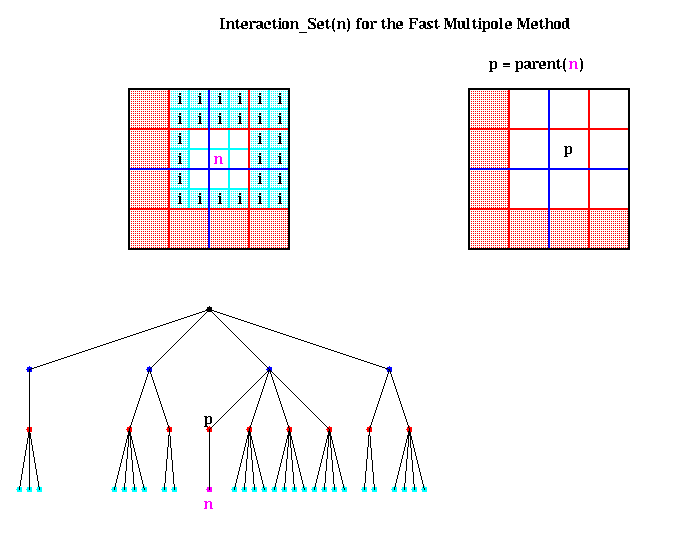
We begin by considering Inner(p), where p is the parent of n, as shown above. By having the algorithm compute parents before children (using a so-called preorder traversal of the quadtree), Inner(p) is already available, and includes the potential due to all particles in the red-shaded region. Computing
Inner_shift( Inner(p), center(n) )
converts this expansion around the center of p to one around the center of n,
which will contribute to Inner(n).
This leaves the particles in the cyan shaded boxes, which are also labeled i for Interaction_Set(n). More formally,
Interaction_Set(n) = { nodes i such that i is a child
of a neighbor of parent(n) but
i is not itself a neighbor of n }
For each node i in Interaction_Set(n), we have Outer(i) available, which
is an accurate expansion inside n. Thus
Convert( Outer(i), center(n) )
gives us an inner expansion for n, which includes the potential due to all
particles inside i. Since there are only a bounded number of nodes i in the
Interaction_set(i) (namely at most 62 - 32 = 27 in 2D, and 63 - 33 = 189
in 3D, with slightly fewer if n is near a boundary of the largest box), there
is only a constant amount of work to do to compute Inner(n). The figure
above also shows Interaction_Set(n) in terms of the quadtree.
We can now state the algorithm for step 3 of the FMM, which is to call Build_Inner(root), where Build_Inner is defined recursively as follows
Build_Inner(n)
p = parent(n) ... p=nil if n=root
Inner(n) = Inner_shift( Inner(p), center(n) )
... Inner(n)=0 if n=root
For all i in Interaction_Set(n)
... Interaction_set(root) is empty
Inner(n) = Inner(n) + Convert( Outer(i), center(n) )
end for
For all children c of n
Build_Inner( c )
end for
Adding inner expansions means just adding their coefficients beta(i),
which is valid, as before, because the potential of a set of particles
is the sum of potentials of each particle alone.
We have skipped some details when the quadtree is adaptive. For example, it may be that some some nodes in the interaction set are not present, because they belong to subtrees containing few points. For example, suppose there were only a few points in the left half of the region above, so the two children of the root on the left were in fact leaves. Then their contribution to node n would not be in computed in step 3, but instead be delayed until step 4 below.
But first we will mention one parallelization of nonadaptive FMM on the Connection Machine CM-2. The CM-2 was an SIMD machine, and so each processor had to execute the same instruction at the same time (or execute nothing). This is clearly not very compatible with an irregularly structured quadtree or octtree, so in this implementation it was assumed that the tree was complete, i.e. every level was fully populated (4i nodes on level i of the quadtree, and 8i nodes on the octtree). This way, the tree traversals in steps 2 and 3 of the FMM could be done in a data parallel fashion, with the same operations at each node on each processor. Thus in step 2, the post-order traversal, all the leaves are processed simultaneously, followed by all their parents, and so on. Step 3, the pre-order traversal, starts with the root, and works its way to the leaves. The communication pattern is very similar to multigrid, as described in Lecture 17.
There have been parallelizations of Barnes-Hut both on shared memory machines and distributed memory machines. On both architectures, two similar strategies have been pursued. Since there is not complete agreement on what to call these strategies, we will make up our own names and call them spatial partitioning and tree partitioning, to distinguish how they divide the work.
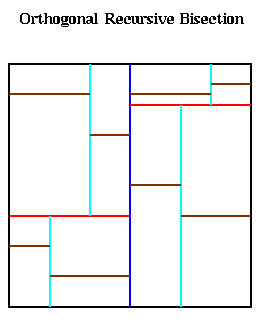
This method divides the large square in which all the particles lie into p nonoverlapping subrectangles, each of which contains an approximately equal number of particles, and assigns each rectangle to a processor. This is also called Orthogonal Recursive Bisection (ORB) in the literature, and is quite similar to the Inertial Bisection algorithm for graphs discussed in Lecture 20. It works as follows. First, a vertical dividing line is found such that half the particles are on one side, and half are on the other, as shown below with the blue line. Next, the particles in the left and right halves are divided in half by horizontal red lines, to get 4 partitions with equally many particles. These are in turn bisected with vertical cyan lines, horizontal brown lines, and so on, until there are as many partitions as processors.
In order for processor k to run Barnes-Hut on the particles it owns, it needs that subset of the quadtree that would be accessed while computing forces for its own particles; this subset is called the Locally Essential Tree (LET). The LET includes the whole subset of the quadtree whose leaves contain the particles inside processor k, as well as "neighboring" tree nodes. Here is an somewhat simplified description of the LET. Recalling the Barnes-Hut algorithm, we let n be a node in the quadtree not containing any particles in processor k, let D(n) be the length of a side of the square corresponding to n, and let r(n) be the shortest distance from any point in n to any point in the rectangle owned by processor k. Then if
(1) D(n)/r(n) < theta and
D(parent(n))/r(parent(n) >= theta,
or
(2) D(n)/r(n) >= theta
n is part of the LET of processor k. The idea behind
condition (1) is that the mass and center of mass of n can be
used to evaluate the force at any point in processor k, but no ancestor of
n in the tree has this property. In particular, no children of n are in the LET.
Condition (2) says we need the ancestors
of all such nodes as well. For an illustration, see
figure 1 on page 3, and figure 3 on page 4, in
"Astrophysical N-body Simulations Using Hierarchical Tree Data
Structures", M. Warren and J. Salmon, Supercomputing 92.
The advantage of conditions (1) and (2) is that processor k can examine its own local subtree, and decide how much of it any other processor j needs for processor j's LET, knowing only the size and location of the rectangle owned by processor j (this is needed to determine r(n)). The parallel algorithm given below for computing the LETs in parallel takes advantage of this.
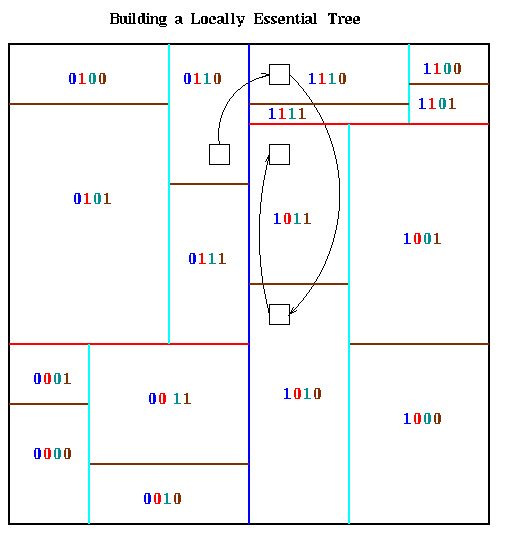
To explain the algorithm, we assume there are p=2m processors. Each m-bit processor number is determined by the orthogonal bisection process; bit i is 1 or 0 depending on the side of the i-th bisecting line on which the processor lies. This is illustrated below for the same partition as above, with bits in processor numbers color coded to indicate to which bisecting line they correspond.
The algorithm below is similar to broadcast on a hypercube, discussed briefly in Lecture 9. It is SPMD code, to be executed by each processor. MYPROC is a variable equal to the local processor number.
Compute local quadtree T
LET = T
for i = 0 to m-1 ... p = 2m
OTHERPROC = MYPROC xor 2i
... flip i-th bit of MYPROC
Compute the subset of LET that any processor on
other side of bisecting line i might want
Send this subset to OTHERPROC
Receive corresponding subset from OTHERPROC, and
incorporate it into LET
end for
prune LET of unnecessary parts
The path a particular part of the quadtree might take to reach its final
destination is circuitous, as illustrated by the small black box in the
last figure. To get from processor 0110 to 1011, which needs it, it
first goes to processor 1110 (leftmost bit flipped), then to processor
1010 (next bit flipped), then it remains in 1010 because it is on the
correct side of the cyan line, and finally it goes to processor 1011
(rightmost bit flipped).
This algorithm was implemented both on the Intel Delta, a distributed memory machine, and the Stanford Dash, a shared memory machine. The Delta implementation was the largest astrophysical simulation ever done at the time, and won the Gordon Bell Prize at Supercomputing 92. The Intel Delta has 512 processors, each one an Intel i860. Over 17 million particles were simulated for over 600 time steps. The elapsed time was about 24 hours, for a sustained flop rate of about 5.2 Gflops. To see results of these simulations, click here.
The shared memory implementation was somewhat slower than the next algorithm, and much more complicated to program.
The shared memory implementation simply used reads of remote data to fetch the parts of the quadtree needed on demand. This data is read-only while traversing the tree to compute forces, and is cached in each processor. Because each processor works on (mostly) contiguous regions of space, the same parts of the quadtree are needed over and over again, so caching is very effective. The speedup was 15 on a 16 processor Dash, which is quite good. (More detailed speedup and scalability studies are in the literature cited below). The disadvantage of the shared memory approach is that cache sizes have to grow proportionally to the number of processors to maintain high efficiency. Also, the locality afforded by this approach is not perfect, as illustrated by the brown processor in the above figure.
The distributed memory algorithm is much more complex, and uses a distributed data structure called a hashed octtree. The idea is to associate a unique key with each node in the quadtree (as before, we limit ourselves to 2D for ease of exposition). Then a hashing function hash(key) will map each key to a global address in a hash table at which to find the data associated with the node. The hash table is then distributed across processors using a technique much like costzones. The hash function permits each processor (with high probability) to find exactly where each node is stored without traversing links in a linked tree structure, and so minimizing the number of communications necessary find get the data at a node.
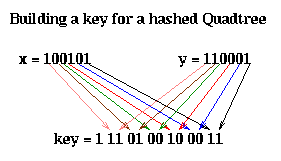
Here is how the key is computed. Let (x,y) be the coordinates of the center of a square. We may think of them as bit strings, as shown below. The corresponding key is obtained by interleaving these bits, from right (least significant) to left (most significant), and putting an extra 1 at the left (to act as a "sentinel").
The nodes at the top of the quadtree are larger, and therefore may be represented by shorter bit patterns. A more complete picture of the keys for each level of the quadtree is shown below. The bits of each key are color coded according to which level of the quadtree determines them.
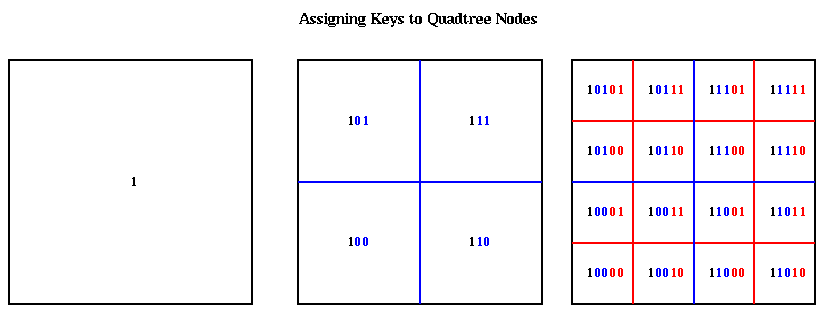
The hash function hash(key) is a simple bit-mask of the bottom h bits of each key. Thus, the top (h/2)+1 quadtree levels ( (h/3)+1 octtree levels) have unique value of hash(key). Each hash table entry include a pointer to a list of boxes with the same value of hash(key), a list of which child cells are actually present, and mass and center of mass data.
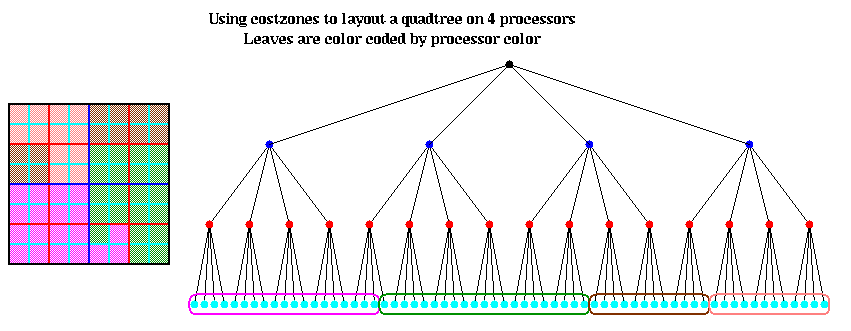
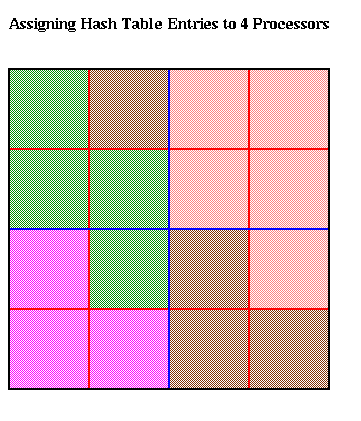
The hash table is partitioned in a method similar to costzones. Suppose h=4, so there is one cell in the hash table for each of the 16 squares on level 3 of the quadtree (the rightmost figure of the three above). Then the keys for each of the 16 squares determine a linear order for these squares, from 10000 to 11111. We want to break this sequence of 16 squares into p contiguous subsequences to assign to processors. To balance the load, we want each each subsequence to require the same work. We do this similarly to costzones, where to each square we associate a cost, and choose the subsequences so the sum of the costs in each subsequence is nearly equal. This is illustrated below, for p=4. Note that a processor may be assigned noncontiguous regions of space, as with costzones. (There are also ways to order the squares using continuous "space-filling curves" which would not lead to noncontiguous regions being assigned to processors. This is discussed in the literature cited below.)
Finally, the Barnes-Hut tree is traversed by sending messages to access remote parts of the hash table. There are many standard techniques to lower the communication needed, including overlapping communication and computation, prefetching parts of the tree, processing tree nodes in the order they become available rather in the order they appear in the tree, and caching.
Here are some performance results from an astrophysics calculation, again on a 512 processor Intel Delta. There are 8.8 million particles, initially uniformly distributed. The time for one Barnes-Hut step is 114 seconds, or 5.8 Gflops. The breakdown of the time is
Decomposing the domain 7 seconds Building the tree 7 seconds Tree traversal 33 seconds Communication during traversal 6 seconds Force evaluation 54 seconds Load Imbalance 7 seconds Total 114 secondsThus, the floating point work of force evaluation takes almost half the time, so the implementation is reasonably efficient. At later stages of the calculation, the particles become highly clustered, and the time increases to 160 seconds, but with about the same timing breakdown as above.