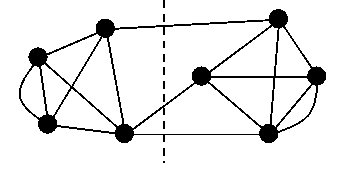
We will spend the next two lectures studying randomized algorithms on graphs. The first problem we will consider is the Min-Cut problem. Given a graph G = (V,E), V the vertices, E the set of edges of G, the minimum cut is the smallest set of edges whose removal breaks G into two pieces. If the size of the minimum cut is k, we say the graph is k-connected. E.g. in the graph below, the minimum cut size is 3, and the graph is 3-connected (which requires in particular that every edge have degree at least 3).

The minimum cut is shown by a dotted line. The cut itself is the set of edges that the dotted line crosses. Note that the graph above is actually a multi-graph, that is, there is more than one edge between some pairs of vertices.
Minimum cuts are in general very useful in parallel programming and divide-and-conquer problem solving. If the graph above represents the communication links between a set of processes at the nodes, then the minimum cut represents a good place to divide the problem between two processors. The minimum cut corresponds to the minimum number of communication links, and so splitting it there minimizes the need for (expensive) communication between processors. Sometimes other criteria are added, e.g. that the two subgraphs induced by the cut have roughly equal size, although we won’t discuss that here.
You probably saw a version of the min-cut problem in CS170 called the s-t min-cut problem. In that problem, you are given two distinguished vertices s and t, and the problem is to find the minimum cut with s on one side and t on the other. The problem we consider here is different in that there are no distinguished vertices. In other words, we are looking for the minimum s-t cut over all pairs s and t.
Contraction is an operation on graphs that reduces an edge to a single vertex. That is, if {x,y} is an edge of the graph to be contracted, then we remove both x and y from the graph, and add a new vertex z. For every edge {u,x} or {v,y} in the original graph, we add an edge {u,z} or {v,z} in the new graph. The result of contracting an edge on the earlier example graph is shown below:
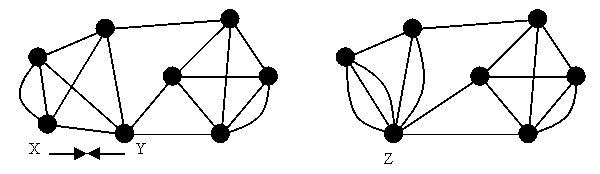
Notice that new multiple edges can result if both x and y are connected to the same vertex before the contraction. That is fine. The graph is a multigraph anyway, and we just keep all the edges that result.
Notice that if the two vertices to be contracted are on the same side of the minimum cut, then the size of the cut does not change. In fact the minimum cut consists of the same edges as before.
On the other hand, contracting two vertices that are on different sides of the minimum cut can change the size and location of the minimum cut. In the example below, the graph is 3-connected before the contraction, but 4-connected after.
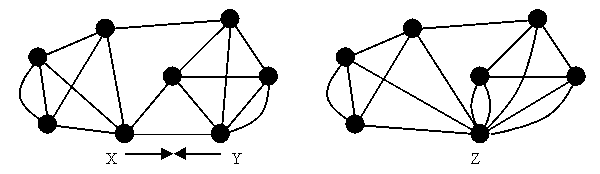
But suppose we were able to always pick vertices x and y which are on the same side of the cut when we do a contraction. The size of the min cut will always stay the same when we do this. Eventually, we would end up with just two vertices, one on each side of the cut. We could not contract these (because they are not on the same side of the cut), and the number of edges between them should still be the size of the minimum cut. The simplest way to choose the vertices x and y to contract is to pick them at random. Let’s call this the "naïve random contraction algorithm". It would look like this:
This algorithm doesn’t seem to have much chance of success but it does better than you might think. In order to output the minimum cut, it must pick at every step an edge that doesn’t cross the minimum cut. Fortunately, the probability that it picks a bad edge on any given step is small, of the order of O(1/n). To see this, first notice that:
In an n-vertex graph G with min-cut of size k, no vertex has degree less than k, and the number of edges in G is at least nk/2.
So when we choose the first edge, the probability that it is one of the k bad edges is k/(nk/2) = 2/n. After we perform a contraction of some edge {x,y}, the new graph has one less vertex, but every vertex in the new graph still has degree at least k. So after i steps, the graph has n-i+1 vertices, so there are at least (n-i+1)k/2 edges in the graph. If we assume that no bad edge has been chosen so far, the probability of choosing a bad edge at the ith step is 2/(n-i+1).
After n-2 steps, we will have just two vertices remaining, and the algorithm will stop. The probability that no bad choices were made at any time is therefore:
![]()
Noting the similarity of these terms to factorials, we write:
![]()
So we have about a 2/n2 chance that running the algorithm will actually find the min cut. If we repeated the algorithm W (n2) times, we would expect to have a good chance of finding the minimum cut on one of them. That gives us an easy Monte-Carlo algorithm: Run the naïve contraction algorithm W (n2) times, keeping track of the size of the smallest cut found so far. With high probability, the min cut will be found, and it will be remembered simply because it will be smaller than cuts found on other executions of the algorithm.
But this is a very slow way to do things. As explained in the text, the contraction algorithm can be implemented to run in O(n2) time, but if we repeat it W (n2) times, the overall running time will be O(n4).
We can try to speed the algorithm up by noticing that the probability of successfully preserving the min cut is given by
![]()
The terms in this product are very close to 1 for small i, but decrease down to 2/3 at the last step. On the other hand, the graph is very small near the end, so it would be possible to find the min cut using a more expensive algorithm.
Suppose we run the algorithm until there are t vertices remaining. Then our probability of success will be
![]()
So for example, if we picked t = Ö n, then we would need approximately n repetitions of the naïve contraction algorithm to have reasonable probability of not losing the min cut. Each of these repetitions would take O(n2) time. After each repetition, we would have a graph with O(Ö n) vertices, and we could find the min cut using standard techniques in time O((Ö n)3) = O(n1.5). The total running time this way would be O(n3) (n repetitions at O(n2) each). This is better than before, but not the best possible.
A more subtle way to speed things up comes from again thinking about how the success probability changes with the step number. Once again, the probability of success is given by the formula:
![]()
In the last method, we simply repeated the naïve contraction algorithm enough times until we had a small graph and then ran a different algorithm. That is, there was just one discontinuity in the algorithm. But even then, the probability of success at the end (assuming we stop at t = Ö n) is only (t-2)/t compared with (n-2)/n at the beginning. That means that the later stages of the naïve algorithm were decreasing our chance of success a lot, forcing us to do a lot of repeats.
A better approach is to gradually boost the probability of success as the problem size gets smaller. How do we do that? Repeat the randomized algorithm! That is, when the graph size gets a bit smaller (by a factor of Ö 2 in fact), we double the number of repetitions of the naïve algorithm. It turns out that keeps our probability of success roughly constant across graph size. We have to examine a lot of graphs, but the number of graphs increases as their size decreases. That’s the ideal trade-off, and the total work we do turns out to be only O(n2). The algorithm looks like this:
First, lets analyze the running time. The algorithm is a straightforward divide-and-conquer, and its running time satisfies:
T = 2T(n/Ö 2) + O(n2)
because there are two recursive calls to instances of size n/Ö 2, and the contraction in the current call takes O(n2) steps. The solution to this recurrence should be familiar from CS170. If not, try drawing a recursion tree with the computational cost at each node. You should find that the total cost at each level of the tree is O(n2). There are O(log n) levels, so the total running time is
O(n2 log n)
But what about the probability of success? The top level of the algorithm runs for n-t steps, from a graph with n vertices down to one with t = n/Ö 2 vertices. The probability that the algorithm succeeds up to this point is
![]()
At the next recursion level, the graph shrinks from n/Ö 2 down to n/2 vertices. The probability of success in going all the way from n down to n/2 vertices is:
![]()
So the probability of success in going from n/Ö 2 down to n/2 vertices, given that we were successful in going from n to n/Ö 2, must be ½. In general, it will always be the case that the probability of successfully going from t vertices to t/Ö 2 is at least ½.
Let P(t) be the probability that a call to the algorithm with t vertices successfully computes the min cut (given that the min cut is still in the graph). Each recursive call on a subgraph Hi succeeds with probability P(t/Ö 2), given that Hi still contains the min cut. The probability that Hi still contains the min cut as we have said is ½. Thus the probability that a recursive call succeeds given that the current graph contains the min cut is ½P(t/Ö 2). But we make two recursive calls, and the probability that at least one of them succeeds is
![]()
This recurrence is tedious but not difficult to solve (see Motwani and Raghavan). After solving, we find that P(n) satisfies:
![]()
So we need to make about log n repetitions of the new algorithm to have a good probability of preserving the min cut. Since each iteration takes only O(n2 log n), that means we can find the min cut in overall time O(n2 log2n).