CS174 Spring 99 Lecture 7 Summary

Stable Marriages and Coupon Collecting

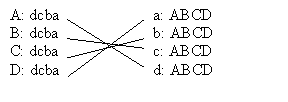
Consider a world with two types of people. Let’s call them male and female. If we start with n males and n females, a marriage is a 1-to-1 pairing of all the males and females.

Each person is assumed to have a preference order for members of the opposite sex. A male A might have preference order dcba, meaning that he prefers d over c, c over b etc. We could write that using a preference function Pref:

A marriage (i.e. a pairing of all the people) is stable if there is no dissatisfied pair. A dissatisfied pair is a male-female combination who like each other more than their current spouses, i.e. if x-X is a married pair and y-Y is another married pair, then X-y would be a dissatisfied pair if

Pref_X(y) > Pref_X(x) and Pref_y(X) > Pref_y(Y)

Example

Here is a stable marriage for 8 people:

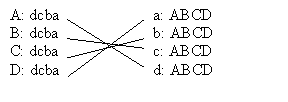
Check for yourself that there is no pair of people who like each other more than their current spouses. Notice that all the males have the same preference order, and so do all the females. That is not necessary, it just makes it easier to understand how the proposal algorithm works (described next). The example in Motwani and Raghavan has different preferences for different people.

The Proposal Algorithm

Surprisingly enough, a stable marriage always exists for any group of equal numbers of males and females. And there is even a straightforward and fairly traditional way of finding it: the proposal algorithm. In the proposal algorithm, a single male proposes to his most-preferred female who has not already turned him down. That female must accept the proposal unless she is married and likes her current spouse more. That means that a single female always accepts a proposal.

Lets work through the proposal algorithm on the example above. Suppose C proposes first. His favorite female is d, and she must accept as a single female so we have:

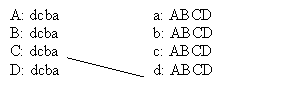
Now suppose B proposes. He will do it to d, even though she is married, and she will accept because she likes him more than C. That leaves C single again:

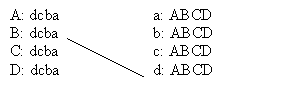
Now if A proposes, he will do it to d, who will accept him, and lose her current husband again. Suppose B proposes again, he will not do it to d this time, because she just divorced him, so this time he tries c. That works out well and they start (what will turn out to be) a long and happy marriage:

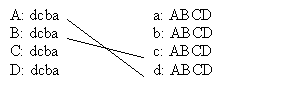
Now C tries again. d has already divorced him, so he tries c instead this time. She rejects him, not just because she is married, but because she prefers her current husband B. So C tries b and this time gets the reply that he hopes for:

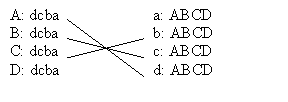
Finally, D chimes in and proposes to d, c, b and after getting rejected every time, has a last try with a. She accepts him, and we arrive at the stable marriage before where everyone is more-or-less happy:

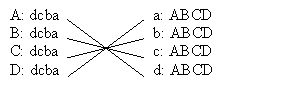
Not everyone gets what they want, but they are at least consoled by the fact that that no-one they want more wants them back.

Analysis

First of all, every male proposes at most once to each female. So the maximum number of proposals is just the number of male-female pairs, which is nxn or n². If the preferences are like the example we just gave, there will actually be about n² proposals. That’s because every male will try the females in the same order, and if k more popular males have gone before them, they will have to try k times before they find a female willing to have them.

Correctness

Its actually fairly easy to show that the proposal algorithm works. The proof is by contradiction.

Suppose there is a dissatisfied pair X-y. Then we must have:

1. Pref_X(y) > Pref_X(x)
2. Pref_y(X) > Pref_y(Y)

Statement 1. means that male X likes y more than his current spouse. He must have proposed to her before, but he isn’t married to her now, so either:

1. She rejected him, which means she liked her then-husband (call him Z) more than X. She was married Y (who might be the same person as Z), so she must have liked him even more. i.e.

Pref_y(X) < Pref_y(Z) <= Pref_y(Y)

But that creates a contradiction with 2.

2. She accepted X at first, but left him later for someone else (call himW) later. Eventually, she was married to Y (who was perhaps W all along), so that means:

Average-case analysis

For some orderings of preferences, the proposal algorithm takes about n² steps. But that was with a rather special ordering of preferences (the same for all males). What about a more "typical" ordering? By typical ordering, we choose each person's preference as a random, uniformly distributed permutation of 1,…,n.

Now its rather hard to analyze this. Instead, rather than picking all those random preference permutations at the beginning, we use a random version of the algorithm to simulate them. This random algorithm, at each step, allows a male to propose to a random female. The name of the female gets added to the end of his preference list as though she had been there on his preference list from the beginning. So its not really the random algorithm that we’re interested in. It's just that the random algorithm behaves just the same as running the normal algorithm with a set of preferences that are uniformly-distributed random permutations. The preference lists get built up during the algorithm. You should be able to see that you still end up with random, uniformly distributed permutations as the preferences anyway. Also, the random choice isn't different from choosing the highest preferred female that hasn’t been proposed to yet. The random choice with this scheme defines the highest preferred female who hasn’t been proposed to yet.

The only odd case is that since a male proposes to a random female, he might come up with the same female in his preference list twice. If so, the second choice is just removed from his list (as though she had not been picked the second time) and he tries again. The random algorithm is now pretty easy to analyze. We make a few observations:

A female, once married, stays married forever, although not necessarily to the same male.

A female is married if and only if she has been proposed to some time.

Every female is married, and the algorithm stops, if and only if every female has been proposed to.

So to figure out how long the algorithm takes, its enough to figure out how many random choices for proposals to n females it takes before all of them has been proposed to. This is equivalent to the following occupancy problem: If m balls are placed into n bins, how long does it take before every bin is non-empty with high probability?

Coupon Collectors Problem

That occupancy problem is usually stated as the coupon collectors problem. If there are n coupons at a supermarket and you get a random one each time you visit, how many (m) do you need to have high probability of getting all the coupons?

For the occupancy version, some bin (say bin 1) is empty with probability

For the probability that some bin is empty, we want

Pr[E₁ Ú E₂ Ú E₃ Ú …Ú E_n] £ Pr[E₁]+Pr[E₂]+…+Pr[E_n]

Which is less than or equal to

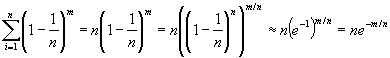
If we set that probability to say 0.01, then we have an inequality

taking logs to base e,

and rearranging:

So if m is somewhat bigger than n ln(n), we have a very good chance of hitting all the bins. So if you make about n ln n visits to the supermarket, you have a good chance to get all n coupons.

Finally, the result that we were interested in: After about n ln n proposals under the random algorithm, every female will have been proposed to, and a stable marriage will result. That means if you started with random permutations as preferences, the proposal algorithm would run for about n ln n steps.