Problem 1. (7 points) Quickies.
a. The minimax algorithm could be said to be using either a preorder or a postorder tree traversal. (Either answer was accepted as correct.)
b. The maximum height of an n-node binary search tree is n - 1.
c. Pruning does not affect the answer produced by minimax.
d. x2z + xy.
e. Use two hash tables; one for authors and one for publishers.
f. None. Because of the finally clause, the only exception that can be thrown is a NullPointerException, which is unchecked.
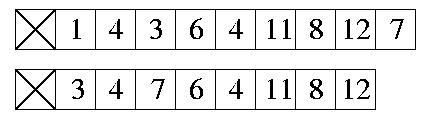
Problem 2. (6 points) Data Structures.
a.

b.
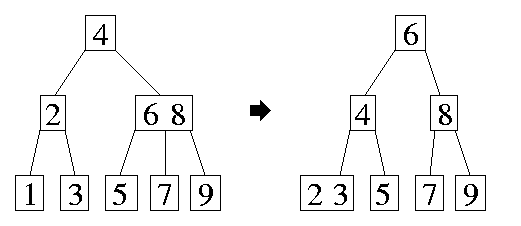
c.
Problem 3. (4 points) Merging Trees.
Set T's root to be the root of R. Find the node in R with maximum key. Set that node's right child to be the root of S.
Problem 4. (8 points) Inserting a Key into a Binary Heap.
public void insertItem(int key) {
int i = size + 1;
while ((i > 1) && (key < heapArray[i / 2])) {
heapArray[i] = heapArray[i / 2];
i = i / 2;
}
heapArray[i] = key;
size++;
}