Jonathan's research

The importance of mesh generation. One of the central tools of scientific computing is the forty-year old finite element method—a numerical method for approximating solutions to partial differential equations. The finite element method is used to develop computer simulations of a wide variety of physical phenomena, including fluid flow, heat transfer, mechanical deformation, and electromagnetic wave propagation. It is used heavily in industry and science for marvelously diverse purposes—determining optimal pumping strategies for petroleum extraction, anticipating the electromagnetic behavior of integrated circuits, studying phenomena from quantum mechanics to earthquakes to black holes. The major automakers invest heavily in finite element software and expertise to help design engines and study the aerodynamics of car bodies. The aerodynamic response of the Boeing 777 airplane was simulated by the finite element method before even the first reduced-scale physical model was constructed for wind tunnel tests.

Joe F. Thompson, a celebrated engineer who commanded a multi-institutional mesh generation project known as the National Grid Project, wrote in 1992 that

An essential element of the numerical solution of partial differential equations (PDEs) on general regions is the construction of a grid (mesh) on which to represent the equations in finite form. The grid must be generated for the regions of interest, and this is far from being a trivial problem. In fact, at present it can take orders of magnitude more man-hours to construct the grid than it does to perform and analyze the PDE solution on the grid. This is especially true now that PDE codes of wide applicability are becoming available, and grid generation has been cited repeatedly as being a major pacing item. The PDE codes now available typically require much less esoteric expertise of the knowledgeable user than do the grid generation codes.

Sixteen years later, mesh generation is still usually the bottleneck in solving PDEs on objects or domains with complicated geometry. The automatic mesh generation problem is to program a computer to divide a complicated geometry—say, a car engine, an apartment building, or the air around an airplane—into simple pieces called elements, such as triangles or rectangles (for two-dimensional geometries), or tetrahedra or rectangular prisms (for three-dimensional geometries). The division may yield millions or billions of such elements, in which case it is infeasible for a human to interactively help the computer with its decisions; the solution must be found entirely automatically.

Mesh generation is something like a reverse jigsaw puzzle. A mesh must satisfy nearly contradictory requirements: it must conform to the shape of the object or domain; it may have to grade from small to large elements over a relatively short distance; and it must be composed of elements that are of the right sizes and shapes. “The right shapes” typically include elements that are nearly equilateral, and exclude elements that are long and thin (e.g. shaped like a needle or a kite). Some versions of the mesh generation problem—for example, dividing an arbitrary three-dimensional domain into “nicely shaped” hexahedra (elements shaped like rectangular prisms, though the sides need not be parallel)—are widely believed to have no general solution.

Since Thompson wrote his article, the resources committed to mesh generation have expanded rapidly. The field has seen the birth of three dedicated conferences: the annual International Meshing Roundtable, the biennial Symposium on Trends in Unstructured Mesh Generation, and the biennial International Conference on Numerical Grid Generation in Computational Field Simulations. Dozens of companies market mesh generation software. Many of the national research laboratories and most of the large automakers have in-house efforts.

Mesh generation is truly an interdisciplinary topic. Most of the early work was done by researchers from several branches of engineering, especially mechanics and fluid dynamics. Unfortunately, mesh generation is such a difficult problem that all the algorithms developed during this period are fragile, and often fail to function when confronted by small domain features, faces meeting at small angles, or complicated topologies that were not anticipated by the programmer.

Around the time of Thompson's article, these problems attracted the interest of researchers in computational geometry. Whereas engineers were once satisfied with mesh generators that (usually) work for their particular domains, those of us in computational geometry pursue a more difficult goal: provably good mesh generation, the design of algorithms that are mathematically guaranteed to produce a satisfying mesh of any geometric domain —even one unimagined by the algorithm designer.

Meanwhile, the applications of mesh generation software have expanded far beyond their provenance. As computers have grown more powerful, triangulated surface models have become widely used in computer graphics, and graphics conferences have seen an explosion of work in mesh generation and geometry processing, including a new conference, the Symposium on Geometry Processing. By economic measures, the computer graphics and animation industry probably now exceeds the finite element industry as a user of meshes.

More generally, meshes are used for hundreds of applications of multivariate interpolation. For example, if a cartographer knows the altitudes of the ground at a finite number of locations, she can generate a mesh of triangles whose corners lie at those locations, estimate the altitude at any other point (where an altitude measurement was not taken) by interpolation, and generate a contour map of the terrain. 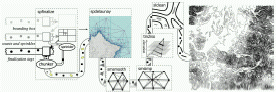Meshes are used heavily in geographic information systems (GIS), image processing, radio propagation analysis, and countless other applications.

For a broad survey of meshes in engineering, graphics, GIS, geometric modeling, theoretical computer science, and more, see the web page for my graduate class on mesh generation and geometry processing.

My work in mesh generation. I implemented a popular two-dimensional mesh generator called Triangle and developed one of the earliest provably good three-dimensional mesh generation algorithms (the first to be as practical as the non-guaranteed algorithms).

My student François Labelle and I developed the first provably good algorithm for anisotropic triangular mesh generation and a guaranteed-quality meshing algorithm called isosurface stuffing that fills smooth surfaces with high-quality tetrahedra. Our isosurface stuffing algorithm represents a major theoretical breakthrough that has eluded researchers for nearly two decades: a mesh generation algorithm for complicated shapes that offers theoretical guarantees on dihedral angles strong enough to be meaningful to practitioners.

My student Bryan Klingner and I developed tetrahedral mesh improvement methods and software that represents a major practical breakthrough: we can produce meshes that usually have far better quality than those produced by any previous algorithm for mesh improvement or mesh generation. The same methods can produce startlingly good anisotropic meshes, and create new possibilities for meshes that change dynamically to model grossly deforming objects.

My work extends from fundamental combinatorial geometry to software implementation.

Software for triangular mesh generation. The 1990s brought about two-dimensional Delaunay refinement algorithms that not only work well in practice, but have provable bounds on element quality and mesh grading. My mesh generator Triangle is an industrial-strength implementation of two-dimensional Delaunay refinement, based on a combination of algorithms by Jim Ruppert, Paul Chew, and myself. Triangle has been freely available to the public since 1995, and has undergone several revisions, most recently in 2005.

Triangle is downloaded from the Netlib repository of mathematical software an average of 31 times a day, and was downloaded over 75,000 times between 1995 and 2004. (More recent figures are not available.) The software has thousands of users (including many hundreds I have heard from personally), and has been licensed for inclusion in eighteen commercial software products. Commercial licensees use Triangle for tasks like digital ink and paint and compositing for cartoon animation, cloth animation (in Alias|Wavefront's well-known Maya computer animation package), surveying and geographical data processing, visualizing three-dimensional ocean floor models, mapping and contouring of subsurface geology and geophysics, and finite element simulation of groundwater flow, contamination transport, and thermal modeling. Non-commercial users use Triangle (free of charge) for terrain databases for real-time simulations; discontinuity meshing for global illumination; stereographic vision; interpolation of speech signals; and finite element methods for electromagnetic modeling, integrated circuit design, propagation of electric currents through myocardial tissue, transport processes in estuaries and aquifers, and earthquake rupture dynamics; plus hundreds of other applications. In 2003, Triangle received the James Hardy Wilkinson Prize in Numerical Software.

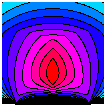
Guranteed-quality anisotropic mesh generation. This work combines a formerly unsolved problem of real importance to mesh generation; a novel theoretical approach; and an algorithm that is practical and the first to be provably good.

Most mesh generation algorithms try to create triangles or tetrahedra that are nearly equilateral. But for some applications of interpolation and numerical modeling, the mesh must be anisotropic: having long, skinny triangles with orientations and aspect ratios dictated by the function being approximated. Engineers using finite elements for applied problems have championed anisotropic meshes increasingly during the last decade. Functions with strongly anisotropic curvature are best interpolated with anisotropic meshes, and partial differential equations that are inherently anisotropic yield the best-conditioned numerical methods if anisotropic elements are used. For example, laminar air flow over an airplane wing is best modeled with extremely thin slab-shaped elements aligned with the surface of the wing. The ideal orientations and aspect ratios of the elements vary (smoothly) from one point in space to another, making anisotropic meshing more difficult than the traditional mesh generation problem.

Delaunay triangulations have mathematical properties that make them excellent for mesh generation, especially provably good mesh generation. However, it appears to be difficult or impossible to adapt Delaunay triangulations to anisotropic metric spaces without losing some of the properties necessary to create an algorithm that is both practical and provably good. Hence, François Labelle and I have developed a novel approach: we eschew the usual idea of constructing and improving a triangulation incrementally. Instead, we have invented a geometric construction that we call an anisotropic Voronoi diagram (a generalization of the well-known multiplicatively weighted Voronoi diagram). See above for an example. Whereas the geometric dual of an ordinary Voronoi diagram is a Delaunay triangulation, the geometric dual of an anisotropic Voronoi diagram is not always a triangulation at all; anisotropic Voronoi diagrams can be quite badly behaved. We can tame an anisotropic Voronoi diagram by inserting new sites at carefully chosen positions, until the geometric dual of the diagram is a guaranteed-quality anisotropic mesh, as illustrated above.

Our algorithm produces a mesh in which no triangle has an angle smaller than 20^o, as measured from the skewed perspective (i.e. metric tensor) of any point in the triangle. This is the first provable guarantee of any kind in anisotropic meshing. François has implemented the algorithm and verified that it produces excellent meshes in practice. The figures above show an anisotropic mesh and the anisotropic Voronoi diagram used to generate it.

Guaranteed-quality tetrahedral mesh generation. I have developed provably good three-dimensional mesh generation algorithms based on Delaunay refinement. The jump from two dimensions to three is surprisingly difficult. Nonetheless, one of my algorithms provably generates a nicely graded mesh whose tetrahedral elements have circumradius-to-shortest edge ratios bounded below 1.63. Unlike previous provably good tetrahedral mesh generation algorithms, my algorithm can mesh general straight-line nonmanifold domains with holes, interior boundaries, and dangling edges and facets—and it works well in practice! (Previous provably good algorithms either generated far too many tetrahedra, or could only mesh convex objects.)

My theoretical results ensure that most types of bad tetrahedra cannot appear in the mesh, but do not rule out the possibility of a bad tetrahedron known as a sliver. Fortunately, Delaunay refinement algorithms outperform their worst-case bounds in practice. Pyramid, my implementation of three-dimensional Delaunay refinement, can usually generate meshes of tetrahedra whose dihedral angles are bounded between 20^o and 150^o.

Isosurface stuffing: guaranteed sliver-free tetrahedral mesh generation for domains with smooth boundaries. François Labelle and I developed an algorithm called isosurface stuffing that fills an isosurface with a uniformly sized tetrahedral mesh whose dihedral angles are bounded between 10.7^o and 164.8^o, as illustrated below, or (with a change in parameters) between 8.9^o and 158.8^o. All vertices on the boundary of the mesh lie on the isosurface. If the isosurface is a smooth 2-manifold with bounded curvature, and the tetrahedra are sufficiently small, then the boundary of the mesh is guaranteed to be a geometrically and topologically accurate approximation of the isosurface.

A 134,400-tetrahedron mesh produced by isosurface stuffing, with cutaway views. At the lower right is a histogram of tetrahedron dihedral angles in 2o intervals; multiply the heights of the red bars by 20. (Angles of 45o, 60o, and 90o occur with high frequency.) The extreme dihedral angles are 15.2o and 158.2o.

The algorithm is whip fast, numerically robust, and easy to implement because, like the well-known Marching Cubes algorithm, it generates tetrahedra from a small set of precomputed stencils. A variant of the algorithm creates a mesh with internal grading: on the boundary, where high resolution is generally desired, the elements are fine and uniformly sized, and in the interior they may be coarser and vary in size. This combination of features makes isosurface stuffing a powerful tool for dynamic fluid simulation, large-deformation mechanics, and applications that require interactive remeshing or use objects defined by smooth implicit surfaces. A drawback of our approach is that it does not preserve sharp edges or corners; it is intended for modeling smooth surfaces, or for simulations in which it is acceptable to round off sharp corners and edges.

Isosurface stuffing is the first tetrahedral mesh generation algorithm of any sort that both offers meaningful bounds on dihedral angles and conforms to the boundaries of geometric domains whose shapes are substantially more challenging than boxes. Significant provable bounds on dihedral angles (1^o or over) are unheard of outside of space-filling or slab-filling tetrahedralizations. We use a computer-assisted proof to guarantee our angle bounds.

We have used isosurface stuffing as part of a method for animating incompressible liquids with free surfaces, illustrated below. For each time step, semi-Lagrangian contouring computes a new fluid boundary (represented as a fine surface triangulation) from the previous time step's fluid boundary and velocity field. Then isosurface stuffing discretizes the region enclosed by the new fluid boundary, creating a tetrahedral mesh that grades from a fine resolution at the surface to a coarser resolution in the interior. Each successive time step entails creating a new triangulated liquid surface and a new tetrahedral mesh. We also use Semi-Lagrangian advection to compute velocities at the current time step on the new mesh. We use a finite volume discretization to perform the pressure projection required to enforce the fluid's incompressibility. The liquid simulation appears in the 2007 Symposium on Computer Animation, and is joint work with Nuttapong Chentanez, Bryan Feldman, François Labelle, and James O'Brien.

Algorithms for tetrahedral mesh improvement. Once you have a tetrahedral mesh that conforms to a geometric domain, you have an opportunity to make its quality a lot better. Bryan Klingner and I have developed a tetrahedral mesh improvement schedule that usually creates meshes whose worst tetrahedra have a level of quality substantially better than those produced by any previous method for tetrahedral mesh generation or “mesh clean-up.” Our goal is to aggressively optimize the worst tetrahedra, with speed a secondary consideration.

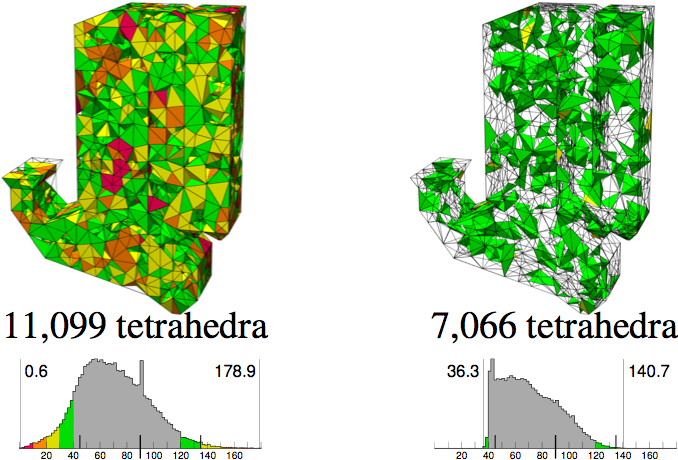The figure at right shows an example of a mesh before and after it is improved by our software. Red tetrahedra have dihedral angles under 10^o or over 165^o, orange have angles under 20^o or over 150^o, yellow have angles under 30^o or over 135^o, green have angles under 40^o or over 120^o, and better tetrahedra do not appear. The histograms show the distributions of dihedral angles, and the minimum and maximum angles, in each mesh. (Histograms are normalized so the tallest bar always has the same height; absolute numbers of tetrahedra cannot be compared between histograms.)

Mesh optimization methods often get stuck in bad local optima (poor-quality meshes) because their repertoire of mesh transformations is weak. We employ a broader palette of operations than any previous mesh improvement software. Alongside the best traditional topological and smoothing operations, we introduce a topological transformation that inserts a new vertex (sometimes deleting others at the same time). We describe a schedule for applying and composing these operations that rarely gets stuck in a bad optimum. We demonstrate that all three techniques—smoothing, vertex insertion, and traditional transformations—are substantially more effective than any two alone.

We show that vertex-creating transformations make it possible to achieve levels of mesh quality that, to the best of our knowledge, are unprecedented. Given meshes whose vertices are somewhat regularly spaced (as every competent tetrahedral mesh generator produces), our implementation usually improves them so that no dihedral angle is smaller than 34^o or larger than 131^o. It sometimes achieves extreme angles better than 41^o or (with a different objective function) 117^o. No previous software we know of for tetrahedral mesh generation or mesh improvement achieves angles of even 14^o or 156^o with any consistency (except my own software Pyramid, which consistently achieves an 18^o lower bound.)

• My papers on mesh generation by Delaunay refinement.
• My papers on non-Delaunay mesh generation and mesh improvement (including isosurface stuffing).
• The Triangle page.

Our two-dimensional streaming triangulator can construct a nine-billion-triangle Delaunay triangulation of a planar point set in eight hours on a laptop computer, using a memory footprint of 166 MB while writing out a 152 GB triangulation. We were surprised and delighted to discover that our software runs about a factor of twelve times faster than the previous best out-of-core Delaunay triangulator. Our three-dimensional triangulator can construct an 815-million-tetrahedron Delaunay triangulation in three hours, using a memory footprint of 800 MB while writing out a 14 GB triangulation. The memory footprint of the 2D triangulator is typically less than 0.5% of the size of its output meshes (sometimes much less). For the 3D triangulator, the figure is usually less than 10%. In other words, we are processing supercomputer-sized meshes on an ordinary laptop.

Streaming computation of Delaunay triangulations in 2D and 3D. Blue quadrants or octants are where future points will arrive. Purple triangles and tetrahedra are in memory. Black points and their triangles and tetrahedra have already been written to disk or piped to the next application.

A key idea is that we store meshes in a streaming mesh format, and points (prior to triangulation) in a streaming point format. Streaming mesh formats contain not only points, triangles, and tetrahedra, but also finalization tags that certify when a topological entity is seen for the last time. Finalization tags permit a geometric algorithm to output partial results and discard associated information, freeing room in memory for more data to stream in. For example, when a vertex finalization tag appears in an incoming stream, it tells the application that no more triangles will arrive that adjoin that vertex. Therefore, the application can complete local processing and perhaps discard the vertex and some of the adjoining triangles, making room for more to stream in. We call this topological finalization, because it depends purely on the connectivity between geometric entities.

The main new idea in our streaming Delaunay triangulators is spatial finalization. We partition space into regions, and include finalization tags in the stream that indicate that no more points in the stream will fall in specified regions. Finalization injects information about the future into a stream—in this case, promises that certain regions contain no additional points. These promises can be used to certify that a tetrahedron's circumsphere is empty, so the tetrahedron is Delaunay and can be safely written to the output stream early, freeing up memory to read more from the input stream. Because only the unfinalized parts of a triangulation are resident in memory, the triangulator's memory footprint remains small.

The triangulations generated by our streaming Delaunay triangulator may be piped directly to another application or visualization tool. Martin Isenburg, during his time as a post-doctoral fellow under my supervision, implemented streaming tools that read streaming meshes and visualize them incrementally (so you can watch the progress of a triangulator), or compute and write information of importance to GIS applications, such as raster Digital Elevation Maps (DEMs) and isolines. We create DEMs from terrain mass points by first triangulating the mass points to create a TIN (Triangulated Irregular Network—GIS-speak for a triangulation), which is used to interpolate elevation values at raster points. Because stream processing modules typically have small memory footprints, we can (and do) run chains of them concurrently on a laptop while streaming gigabytes through them.

• My papers on streaming geometric computation.
• Streaming tools for processing huge geometric data sets, including:
  • Streaming tools for constructing huge Delaunay triangulations.
  • Streaming tools for constructing Digital Elevation Maps and isolines.
  • Streaming tools for processing LIDAR data in LAS format.
  • Streaming tools for visualizing LIDAR data in Google Earth.

My predicates (or variants thereof) are incorporated in several software programs, including the Cart3D inviscid analysis package by Michael Aftosmis, Marsha Berger, and John Melton; the Power Crust surface reconstruction package by Nina Amenta, Sunghee Choi, and Ravi Kolluri; the GNU Triangulated Surface Library (GTS); and the Manifold Code (MC) adaptive multilevel finite element kernel by Michael Holst.

Cart3D is a notable example, used for computational fluid dynamics modeling of aerodynamic behavior in aviation and launch vehicle projects at NASA. Cart3D uses my geometric predicates to robustly prepare surface meshes for simulations that integrate many different physical components. Cart3D played a central role in debris transport analysis of the Columbia space shuttle disaster, as illustrated at right. Cart3D's fluid dynamics simulation was a primary means of determining the size, weight, and impact velocity of the foam that damaged the Columbia's wing.

Triangle and Pyramid both use the robust predicates, which are indispensable in allowing them to generate meshes that had previously been unattainable because roundoff errors had caused the mesh generators to fail.

Happily, Nanevski et al. designed and implemented an expression compiler that generates predicates automatically (in the style of my hand-coded predicates).

• My papers on adaptive precision floating-point arithmetic and robust geometric predicates.
• The Robust Predicates page.

A Delaunay triangulation is the most “natural” triangulation of a point set. Its enduring popularity arises from many favorable properties such as its tendency to consist of “nicely rounded” triangles or tetrahedra, the fact that it is optimal by several useful criteria, the existence of many well-studied algorithms for constructing it quickly, and the fact that modifications are usually local in effect (and thus fast). Delaunay triangulations can be defined in any dimensionality, though the two- and three-dimensional versions are used most heavily in practice.

However, many applications (particularly in graphics, scientific computing, and interpolation) need triangulations of nonconvex objects, or objects that have internal boundaries and discontinuities. For this reason, a two-dimensional geometric construction called the constrained Delaunay triangulation (CDT) was developed in 1986. A CDT is not merely a triangulation of a point set; it is also guaranteed to respect specified segments. Therefore, you can produce a CDT of an object with a complicated nonconvex shape, holes, and interior boundaries (such as the interface between two different materials in a heat conduction simulation). Yet CDTs preserve most of the optimality properties that make Delaunay triangulations so popular.

In 1997, most geometers believed that the CDT could not generalize to three dimensions, however desirable it might be. (CDTs are, in several senses, optimal for piecewise linear interpolation.) A major hurdle is the fact that not all polyhedra can be tetrahedralized without additional vertices. Furthermore, it is NP-hard to determine whether or not a polyhedron can be tetrahedralized without extra vertices, or how many vertices must be added to make it possible.

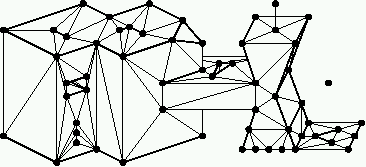
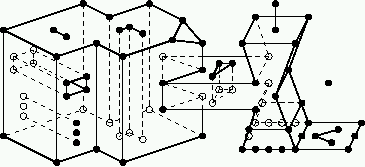In 1998, I published a proof that a three-dimensional domain whose boundaries are flat facets (that are not necessarily convex) has a CDT if a certain mathematical condition holds. The figure at right shows a domain and its CDT. This condition is easily tested by a simple algorithm, and the existence result extends to higher dimensions. When the condition does not hold, it can be enforced by a simple algorithm that inserts extra, carefully chosen vertices in a way that guarantees that unnecessarily short edges are not created—thereby making CDTs an ideal foundation for three-dimensional mesh generation. Recall that two-dimensional domains with small angles are difficult to mesh well. Small angles present even greater problems in three dimensions. CDTs provide a way to extend provably good Delaunay mesh generation to domains with small angles (both planar and dihedral angles). Because real-world domains have small angles, this makes all the difference between a merely theoretical algorithm and a practical one.

The next problem was to find a good algorithm for constructing CDTs—one that is both fast and easy to implement. In 2000, I published a sweep algorithm, the first algorithm to be fast enough for practical use. In 2003, I published an algorithm based on bistellar flips; it is simpler and even faster than the sweep algorithm. I am currently incorporating the flip algorithm into Pyramid. I believe the inclusion of CDTs will make the software robust enough for public distribution.

I have also discovered that my existence proofs and construction algorithms can be adapted to a more general class of triangulations known as constrained regular triangulations, or weighted CDTs. Other innovations include simple algorithms for inserting a vertex or facet into a CDT, deleting a vertex or facet from a CDT, and finding a single simplex of a CDT through linear programming. A surprising result, discovered in collaboration with visiting student Nicolas Grislain (of the École Normale Supérieure de Lyon), is that it is NP-hard to determine whether a domain has a CDT, even though it can be determined in polynomial time under the “general position” assumption that no five vertices lie on a common sphere!

• My papers on higher-dimensional constrained Delaunay triangulations.

When I began to learn about scientific computing and mesh generation, I wanted to find an article that would explain to me the connection between the geometry of a mesh and the results obtained by an application that uses the mesh. To my surprise, I could not find such an article. After eight years of searching, I decided to write one myself.

When I began the article, I was further surprised to discover that many of the results I wanted to survey do not seem to be in the literature. Hence, my “survey” has entailed much original research too, primarily on the error analysis of piecewise linear interpolation applied to isotropic and anisotropic functions over triangles and tetrahedra.

Some of my new results are on quality measures for meshes. A quality measure is a formula used to determine the quality of a triangle or tetrahedron; it is used as an objective function in algorithms for improving meshes by numerical or combinatorial optimization. Strange as it may seem, most publications on quality measures in the mesh generation literature establish no direct mathematical connection between the quality measures they propose and the goals of the application! In the 2002 International Meshing Roundtable, I published an excerpt that derives quality measures directly from the worst-case interpolation error that an element may suffer (and from other considerations, like stiffness matrix condition number). My error bounds for gradients interpolated over triangles and tetrahedra are tighter than any that have previously appeared in the published literature.

The full-length paper, still in progress, is a survey of the relationship between mesh geometry, interpolation errors, stiffness matrix conditioning, and discretization errors, as well as quality measures. It also treats the circumstances where anisotropic meshes are needed, either because a solution function has anisotropic curvature, or because a partial differential equation is inherently anisotropic. These results played a crucial role in defining the problem solved by our anisotropic meshing algorithm.

• My papers on element quality.

• My papers on the Quake Project.
• All papers for the Quake Project.
• The Quake Project page.
• The Archimedes page.

Jonathan Shewchuk