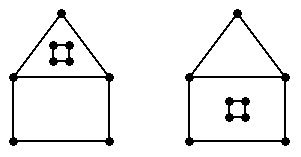
Figure 1: Two PSLGs which are topologically different if we consider the 2-faces to be part of the topology.
[1] The quad-edge data structure (1 point). Each quad-edge has four Data fields, two of which can be used to indicate the 2-faces adjoining the quad-edge. The two PSLGs in Figure 1 may be distinguished by checking whether the small square hole shares a face with the triangular region, or with the quadrilateral region.

[2] Deloopsy (1 point). Two bad examples are illustrated in Figure 2. The example on the right is more relevant, because the algorithm was published as a method of retriangulating the void left behind when a vertex is deleted from a Delaunay triangulation.
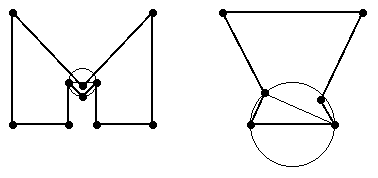
[3] An upper bound on two-dimensional triangulations I (1 point). Rotate the triangulation so no two vertices have the same x-coordinate. Name the three vertices of each triangle the left vertex, the middle vertex, and the right vertex in order according to their x-coordinates. Each vertex is the middle vertex of at most two triangles: the one immediately above it, and the one immediately below it. Hence, if there are n vertices, there are no more than 2n triangles.
Suppose that the outer face of the triangulation has three vertices. The left and right vertices of the outer face have no triangle immediately above or below them. The middle vertex of the outer face can have a triangle above it or a triangle below it, but not both. Thus, for a triangular outer face, there are at most 2n - 5 triangles. If the outer face has more than three vertices, then the number of triangles can only be smaller.
[4] An upper bound on two-dimensional triangulations II (1 point).
A triangulation of n vertices with only three vertices on the boundary
can be created for any
![]() --for
instance, by lazy triangulation.
Observe that every vertex not on the boundary has one triangle
directly above it and one triangle directly below it,
and is the only middle vertex of those two triangles,
so there must be at least 2(n - 3) distinct triangles
in such a triangulation.
Similarly, the middle vertex of the outer face has one triangle either
directly above it or directly below it,
and is the unique middle vertex of that triangle,
bringing the total to at least 2n - 5.
--for
instance, by lazy triangulation.
Observe that every vertex not on the boundary has one triangle
directly above it and one triangle directly below it,
and is the only middle vertex of those two triangles,
so there must be at least 2(n - 3) distinct triangles
in such a triangulation.
Similarly, the middle vertex of the outer face has one triangle either
directly above it or directly below it,
and is the unique middle vertex of that triangle,
bringing the total to at least 2n - 5.
[5] Gift-wrapping gaffes (1 point). Gift-wrapping may unwittingly reduce the untetrahedralized region between six cospherical vertices to a void shaped like Schönhardt's polyhedron, making it impossible to complete the Delaunay tetrahedralization.
[6] Fast times with Frankensimplex (1 point).
Chazelle's polyhedron (Bern and Eppstein, page 58)
cannot be tetrahedralized with fewer than
![]() tetrahedra.
Hence, an
tetrahedra.
Hence, an
![]() time tetrahedralization algorithm is not possible.
time tetrahedralization algorithm is not possible.
[7] Who needs transformations most? (2 points.) Mesh A makes a sudden transition from small to large elements where the advancing fronts collided. The quality of these elements cannot be significantly improved without changing the topology of the mesh. (A transition from small to large elements can easily be identified from the connectivity of a mesh alone, disregarding the locations of the vertices. For example, if you ask how many vertices are within h hops of a vertex in a uniform mesh, the answer grows quadratically with h. If you ask the same question for a vertex on the large side of a rapid transition from large to small elements, the answer grows exponentially. If the base of the exponent is too large, the transition cannot be accomplished with good-quality elements.)
Mesh B has poorly shaped boundary tetrahedra, but many of these occur because the octree cuts the domain too close to the boundary. Smoothing will fix most of the resulting disparities in edge length, and many of the relatively flat elements on the boundary. The excellent quality of the interior elements provides some slack, so that nodes near the boundary can be smoothed without compromising the quality of the interior elements. Some poor boundary tetrahedra may require topological transformations to fix, but their number will be smaller than in Mesh A.
[8] Meshing prespecified boundaries (2 points). Advancing front methods, by nature, work well with pretriangulated boundaries, because they generate elements near the boundary first so that the quality of the boundary elements is as good as possible.
The quadtree approach is ill-suited to pretriangulated boundaries, because intersections of quadtree edges with the domain boundary must be resolved by warping the quadtree so that these intersections occur only at the input vertices. It may not be possible to do this without generating severely distorted elements.
The Delaunay approach falls somewhere in between. It can certainly be made to honor the prespecified boundaries, by the use of constrained Delaunay triangulations. However, if poor-quality elements occur at the boundary, there is no recourse for fixing them.
[9] Minimum spanning trees (2 points). Suppose (v, w) is an edge in the minimum spanning tree T, but vw is not an edge of the Delaunay triangulation. Let D be the smallest disk containing v and w (so that vw is a diameter of D). Because vw is not strongly Delaunay, there must be some other vertex u in D. The line segments uv and uw are shorter than vw.
If (v, w) is removed from T, then T is split into two trees T', which contains v, and T'', which contains w. Without loss of generality, assume u is in T'. If we replace (v, w) with (u, w), we produce a spanning tree whose total edge length is shorter than that of T, contradicting the assumption that T is a minimum spanning tree.
Hence, by contradiction, every edge of the minimum spanning tree is Delaunay.
[10] Constrained mesh smoothing (2 points). If g is the direction of steepest ascent of a smooth function, and gproj is the projection of g onto a plane, then g and gproj are separated by an angle strictly less than 90o (if gproj is nonzero). Hence, the smooth function increases along the direction gproj.
If there is only one angle in the active set,
the utility function we are trying to optimize
(the worst angle) appears locally smooth.
If there are two or more angles in the active set,
the vertex being smoothed lies at a nonsmooth point in the utility function,
and the rules change.
For instance, if g is a linear combination of
![]() and
and
![]() ,
then
,
then ![]() and gproj
might be separated by an angle greater than 90o
(even though g and gproj
are still separated by an angle strictly less than 90o),
as Figure 3 illustrates.
In this case, f1 actually decreases along the direction
gproj.
and gproj
might be separated by an angle greater than 90o
(even though g and gproj
are still separated by an angle strictly less than 90o),
as Figure 3 illustrates.
In this case, f1 actually decreases along the direction
gproj.
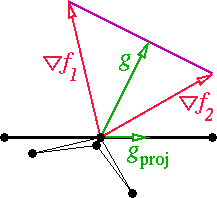
Since the function we want to optimize is the worst angle, and f1 is in the active set, if f1 decreases, our utility function decreases as well.
The fix is to project each vector
![]() ,
,
![]() , etc. onto the facet
before computing the search direction g.
Then, g is the vector of minimum length whose endpoint falls within
the convex hull of the projected vectors.
, etc. onto the facet
before computing the search direction g.
Then, g is the vector of minimum length whose endpoint falls within
the convex hull of the projected vectors.
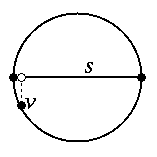
[11] Off-center subsegment splitting (2 points). Let d be the distance from v to s. If the orthogonal projection of v onto s is at least a distance of d from the nearest endpoint of s, then split s at the orthogonal projection. Otherwise, choose a splitting point a distance of d from the nearest endpoint.
This method guarantees that the insertion radius of the new vertex is not smaller than lfsmin. Hence, Theorem 20 still holds.
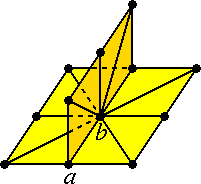
[12] Herbert's typo (2 points). Figure 5 offers an example where the contraction of ab is a local unfolding. Note that a is an order 2 vertex, and b is an order 1 vertex.
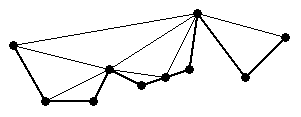
[13] Delaunay triangulation of an x-monotone chain (4 points). Name the three vertices of each triangle the left vertex, the middle vertex, and the right vertex in order according to their x-coordinates. Every triangle above the chain is above its middle vertex, and so it is above two of its edges (see Figure 6).
Let ab be an edge (with a to the left of b) that is either an input edge or has been created by the algorithm. If ab is not on the boundary of the convex hull, let abc be the Delaunay triangle immediately above ab, and let d be any other vertex above the line that contains ab. Because abc is Delaunay and no four vertices are cocircular, c is inside the circumcircle of abd, and abd is not Delaunay. A circumcenter is equidistant from the vertices of its triangle, so the circumcenters of abc and abd both lie on the bisector of edge ab. Because a and b have different x-coordinates, the bisector is not horizontal. Because c and d are both above the line containing ab, and c is inside the circumcircle of abd, the circumcenter of abc is below the circumcenter of abd. (Think of Guibas and Stolfi's rising bubble: starting with the circumcircle of abc, move the circle's center upward along the bisector of ab until the circle touches d.)
It follows that the circumcenter of abc is lower than the circumcenter of any non-Delaunay triangle atop ab that might be placed in the priority queue Q. Hence, if every Delaunay triangle is created as soon as the sweepline passes over its circumcenter, no non-Delaunay triangle can ever be created.
In the Voronoi dual of a Delaunay triangulation, every Delaunay triangle dualizes to its circumcenter, and every Voronoi edge is orthogonal to its dual Delaunay edge. Hence, every triangle above the chain has a circumcenter incident on two Voronoi edges going down to the circumcenters of the two triangles immediately beneath it (if two such triangles exist), and one Voronoi edge going up to the circumcenter of the triangle immediately above it (if such a triangle exists).
Let t be any Delaunay triangle above the chain. Assume for the sake of induction that every triangle whose circumcenter is lower than t's was created when the sweepline passed over its circumcenter. Then both of t's lower edges are created before the sweepline passes over t's circumcenter, because each of t's lower edges is either an input edge, or an edge of a Delaunay triangle with a lower circumcenter. When the second of these edges is created, t is entered on Q. Hence, t is created when the sweepline passes over its circumcenter.
[14] Nearest neighbors in curve reconstruction (4 points). For the sake of contradiction, suppose some point x and its Euclidean nearest neighbor y are not adjacent along the curve F.
Let D be the smallest disk containing x and y (so that xy is a diameter of D), as Figure 7 illustrates. Because y is the nearest neighbor of x, no other vertex lies in D. Because x and y are not adjacent along F, the portion of F incident on x must leave D and pass through some other vertex before it can return to y. Hence, F intersects D in at least two connected components. By Lemma 1 of Amenta, Bern, and Eppstein, D contains a point of the medial axis.
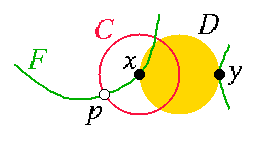
Let l be the distance between x and y. Let C be a circle centered at x whose radius is 0.5 l. Let p be a point on the intersection of C and the curve F. The distance between p and the medial axis point in D is at most 1.5 l. If the point set 0.3-samples F, then some sample point must lie within a distance of 0.45 l of p. Both x and y are a distance of at least 0.5 l from p, so the sample point must be a distinct vertex z, which lies within a distance of 0.95 l from x. This contradicts the assumption that y is the nearest neighbor of x.
[15] Triangulate a PSLG in ![]() time (4 points).
Assume we have rotated the plane infinitesimally so that no segment
is perfectly horizontal.
time (4 points).
Assume we have rotated the plane infinitesimally so that no segment
is perfectly horizontal.
Anywhere the pseudocode says "if helper(e) is a merge vertex," we must reinterpret "merge vertex" to include any vertex that does not have an segment going down (including zero-degree vertices).
A vertex with degree one is either the lower endpoint of a segment, and can be treated exactly like a merge vertex, or is the upper endpoint of a segment, and can be treated exactly like a split vertex.
Zero-degree vertices may be handled by the following pseudocode.
HANDLEZERODEGREEVERTEX(vi) 1 Find the segment ej to the left of vi (by tree search) 2 create the diagonal vi-helper(ej) 3 helper(ej)The remaining vertices we must account for are the degree-two vertices that have the interior region on both sides of their segments, and the vertices of degree three or more. For these vertices, use the following procedure. Partition the incident segments into those going up from the vertex, and those going down. Sort each of these two sets from left to right.vi
Now, iteratively treat vi like a start, end, split, merge, or regular vertex as many times as necessary to process each adjacent pair of edges incident on vi for which the region between the pair of edges is in the interior of the region to be triangulated. For each adjacent pair of upward segments, if the region between them is interior, treat vi like an end vertex for that pair of segments. If vi has no downward segments, but the region below it is interior, treat vi like a merge vertex for the leftmost and rightmost segments. If vi has no upward segments, but the region above it is interior, treat vi like a split vertex for the leftmost and rightmost segments. If vi has at least one upward and one downward segment, and the region to its left is interior, treat vi like a regular vertex; repeat for the region to its right if that is interior. For each adjacent pair of downward segments, if the region between them is interior, treat vi like a start vertex for that pair of segments.