Papers Presented by Students

|
CS 294-5: Meshing and Triangulation (Autumn 1999) Papers Presented by Students |
Please have a date assigned to you no later than September 28. You are welcome to choose only a date now, and put off choosing the paper until up to a week before your date. However, papers are assigned first-come first-served. You are also welcome to choose a relevant paper not on this list (and you are encouraged to do so if it is helpful to your own research), but you must provide me with a copy one week before your presentation. You may change your mind about what paper to present up to a week before your presentation, but please let me know as early as possible.
There is time for two student presentations on each available date. When a student chooses a date and paper, I'll put their name next to each below, so that you'll know which dates and papers were already taken last time I updated this page.
Your presentation should take 25 to 30 minutes. Don't feel you must present everything in a paper; rather, concentrate on presenting the most interesting or important parts. Give theoretical proofs (if any) only if you think you can present them well in the time allotted.
Please use the overhead projector for your presentation if possible. I will try to make blank write-on transparencies available, if I can lay my hands on enough of them. (If I can't, you'll have to buy your own. Ditto for photocopies of figures in the papers.)
Thursday, October 7 -
Jason Riedy, Andy Neureuther.
Thursday, October 21 - Jae Kim, Borlin Shyu.
Tuesday, November 2 -
Dan Simkins, Jordan Smith.
Thursday, November 4 -
Michael Downes, Ganping Sun.
Tuesday, November 9 -
Tolga Goktekin, Okan Arikan.
Thursday, November 11 -
François Labelle, Maryann Simmons.
Tuesday, November 16 - Steve Chien, Jane Wang.
Thursday, November 18 -
Yan Zhuang, Chris Tchou.
Tuesday, November 23 - Tzi-cker Chiueh.
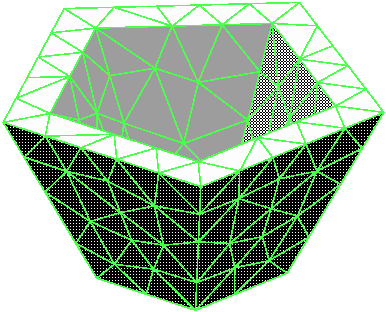
 Guy E. Blelloch, Gary L. Miller, and Dafna Talmor,
Developing a Practical Projection-Based Parallel Delaunay Algorithm,
Proceedings of the Twelfth Annual Symposium on Computation Geometry
(Philadelphia, Pennsylvania), pages 186-195, ACM, May 1996.
PostScript.
Slides from Dafna's
talk (PostScript) are also available.
François Labelle.
Guy E. Blelloch, Gary L. Miller, and Dafna Talmor,
Developing a Practical Projection-Based Parallel Delaunay Algorithm,
Proceedings of the Twelfth Annual Symposium on Computation Geometry
(Philadelphia, Pennsylvania), pages 186-195, ACM, May 1996.
PostScript.
Slides from Dafna's
talk (PostScript) are also available.
François Labelle.
This is the only parallel Delaunay triangulation algorithm I am aware of
that is good in both theory and practice.
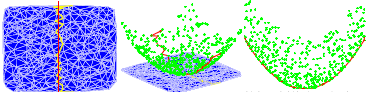
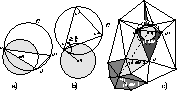 Olivier Devillers,
Improved Incremental Randomized Delaunay Triangulation,
Proceedings of the Fourteenth Annual Symposium on Computation Geometry
(Minneapolis, Minnesota), pages 106-115, ACM, June 1998.
PostScript.
Also check out the
technical report (PostScript)
by the same name, which has bigger figures (better for photocopying)
and perhaps more useful information. Jae Kim.
Olivier Devillers,
Improved Incremental Randomized Delaunay Triangulation,
Proceedings of the Fourteenth Annual Symposium on Computation Geometry
(Minneapolis, Minnesota), pages 106-115, ACM, June 1998.
PostScript.
Also check out the
technical report (PostScript)
by the same name, which has bigger figures (better for photocopying)
and perhaps more useful information. Jae Kim.
This paper describes an interesting randomized dynamic point location method
for incremental Delaunay triangulation.
It works with vertex deletions, as well as insertions.
Good in both theory and practice.
You may want to consider implementing this paper as your "something extra"
for Project I.
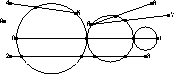 Herbert Edelsbrunner and Tiow Seng Tan,
An Upper Bound for Conforming Delaunay Triangulations,
Discrete & Computational Geometry 10(2):197-213, August 1993.
PostScript.
Herbert Edelsbrunner and Tiow Seng Tan,
An Upper Bound for Conforming Delaunay Triangulations,
Discrete & Computational Geometry 10(2):197-213, August 1993.
PostScript.
This is the paper that gives an algorithm that achieves the best known bound
for the number of Steiner points needed to create a Delaunay triangulation
that conforms to a specified PSLG.
For a brief description of this result, see Bern and Eppstein, pages 37-38.
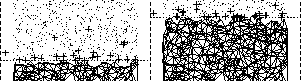 Peter Su and Robert L. Scot Drysdale,
A Comparison of Sequential Delaunay Triangulation Algorithms,
Proceedings of the Eleventh Annual Symposium on Computational Geometry
(Vancouver, British Columbia, Canada), pages 61-70, ACM, June 1995.
PostScript.
You might also want to look at Chapter 2 of
Peter Su's dissertation (PostScript)
for additional figures and algorithmic details.
Maryann Simmons.
Peter Su and Robert L. Scot Drysdale,
A Comparison of Sequential Delaunay Triangulation Algorithms,
Proceedings of the Eleventh Annual Symposium on Computational Geometry
(Vancouver, British Columbia, Canada), pages 61-70, ACM, June 1995.
PostScript.
You might also want to look at Chapter 2 of
Peter Su's dissertation (PostScript)
for additional figures and algorithmic details.
Maryann Simmons.
This is the best extant comparison of the speed of
two-dimensional Delaunay triangulation algorithms.
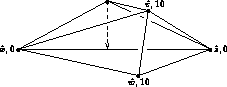 Marshall Bern, Herbert Edelsbrunner, David Eppstein, Scott Mitchell,
and Tiow Seng Tan,
Edge Insertion for Optimal Triangulations,
Discrete & Computational Geometry 10:47-65, 1993.
PostScript.
Marshall Bern, Herbert Edelsbrunner, David Eppstein, Scott Mitchell,
and Tiow Seng Tan,
Edge Insertion for Optimal Triangulations,
Discrete & Computational Geometry 10:47-65, 1993.
PostScript.
This paper shows how to construct a triangulation that
minimizes the maximum angle
(whereas the Delaunay triangulation maximizes the minimum angle).
You will need to be selective about which parts of this paper to present.
Ideally, try to convey an intuition of why this algorithm
can minimize the maximum angle.
For a brief description of this result, see Bern and Eppstein, pages 14-17.
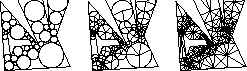 Marshall Bern, Scott Mitchell, and Jim Ruppert,
Linear-Size Nonobtuse Triangulation of Polygons,
Discrete & Computational Geometry 14:411-428, 1995.
PostScript.
Marshall Bern, Scott Mitchell, and Jim Ruppert,
Linear-Size Nonobtuse Triangulation of Polygons,
Discrete & Computational Geometry 14:411-428, 1995.
PostScript.
How to triangulate a polygon so that no angle is larger than 90 degrees.
For a brief description of this result, see Bern and Eppstein, pages 29-30.
The paper mentions a cubic-time algorithm for finding the MWT of a polygon (rather than a point set, for which no polynomial algorithm is known). This algorithm can be found in Bern and Eppstein, pages 17-18.
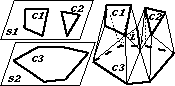 Chandrajit L. Bajaj, Edward J. Coyle, and Kwun-Nan Lin,
Surface and 3D Triangular Meshes from Planar Cross Sections,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 169-178, October 1996.
PostScript. Jane Wang.
Chandrajit L. Bajaj, Edward J. Coyle, and Kwun-Nan Lin,
Surface and 3D Triangular Meshes from Planar Cross Sections,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 169-178, October 1996.
PostScript. Jane Wang.
How to reconstruct the surface or volume of a solid given only
planar cross sections of it.
 Frank Bossen and Paul Heckbert,
A Pliant Method for Anisotropic Mesh Generation,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 63-74, October 1996.
PostScript.
Slides from a related
talk (PostScript) by Paul are also available.
Frank Bossen and Paul Heckbert,
A Pliant Method for Anisotropic Mesh Generation,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 63-74, October 1996.
PostScript.
Slides from a related
talk (PostScript) by Paul are also available.
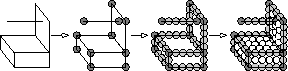 Kenji Shimada,
Anisotropic Triangular Meshing of Parametric Surfaces via
Close Packing of Ellipsoidal Bubbles,
Sixth International Meshing Roundtable (Park City, Utah),
pages 375-390, October 1997.
PostScript. Ganping Sun.
Kenji Shimada,
Anisotropic Triangular Meshing of Parametric Surfaces via
Close Packing of Ellipsoidal Bubbles,
Sixth International Meshing Roundtable (Park City, Utah),
pages 375-390, October 1997.
PostScript. Ganping Sun.
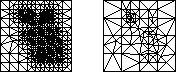 Marshall Bern, David Eppstein, and John R. Gilbert,
Provably Good Mesh Generation,
Journal of Computer and System Sciences 48(3):384-409, June 1994.
PostScript.
Marshall Bern, David Eppstein, and John R. Gilbert,
Provably Good Mesh Generation,
Journal of Computer and System Sciences 48(3):384-409, June 1994.
PostScript.
This classic paper gives the first size-optimal guaranteed-quality
meshing algorithm. It's based on quadtrees.
For a brief description of this result, see Bern and Eppstein, pages 22-25.
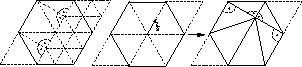 Friedhelm Neugebauer and Ralf Diekmann,
Improved Mesh Generation: Not Simple But Good,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 257-270, October 1996.
PostScript.
Friedhelm Neugebauer and Ralf Diekmann,
Improved Mesh Generation: Not Simple But Good,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 257-270, October 1996.
PostScript.
An improvement to the Bern, Eppstein, and Gilbert algorithm
that uses a rhomboidal quadtree.
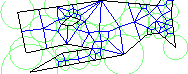 Marshall Bern and David Eppstein,
Quadrilateral Meshing by Circle Packing,
Sixth International Meshing Roundtable (Park City, Utah),
pages 7-19, October 1997.
PostScript.
Marshall Bern and David Eppstein,
Quadrilateral Meshing by Circle Packing,
Sixth International Meshing Roundtable (Park City, Utah),
pages 7-19, October 1997.
PostScript.
An algorithm for creating quadrilateral meshes with no angles larger than
120 degrees.
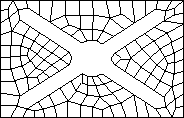 Paul Kinney,
CleanUp: Improving Quadrilateral Finite Element Meshes,
Sixth International Meshing Roundtable (Park City, Utah),
pages 449-461, October 1997.
PostScript.
Paul Kinney,
CleanUp: Improving Quadrilateral Finite Element Meshes,
Sixth International Meshing Roundtable (Park City, Utah),
pages 449-461, October 1997.
PostScript.
How to apply topological transformations to improve an existing
quadrilateral mesh.
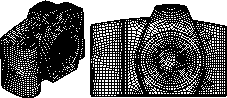 Steven J. Owen, Matthew L. Staten, Scott A. Canann, and Sunil Saigal,
Advancing Front Quadrilateral Meshing Using Triangle Transformations,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 409-428, October 1998.
PostScript. Dan Simkins.
Steven J. Owen, Matthew L. Staten, Scott A. Canann, and Sunil Saigal,
Advancing Front Quadrilateral Meshing Using Triangle Transformations,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 409-428, October 1998.
PostScript. Dan Simkins.
This appears to be a particularly good paper on quadrilateral mesh generation.
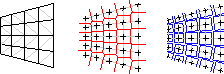 Kenji Shimada, Jia-Huei Liao, and Takayuki Itoh,
Quadrilateral Meshing with Directionality Control through the
Packing of Square Cells,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 61-75, October 1998.
PostScript.
Kenji Shimada, Jia-Huei Liao, and Takayuki Itoh,
Quadrilateral Meshing with Directionality Control through the
Packing of Square Cells,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 61-75, October 1998.
PostScript.
Bubble meshing ideas applied to quadrilateral meshes.
 Ted Blacker,
The Cooper Tool,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 13-29, October 1996.
PostScript. Steve Chien.
Ted Blacker,
The Cooper Tool,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 13-29, October 1996.
PostScript. Steve Chien.
The most common technique for generating a hexahedral mesh is sweeping
a quadrilateral mesh along the third axis.
This technique only works well if the object being meshed is nicely structured.
Here's a relatively sophisticated discussion of how to make sweeping work
on complicated shapes.
 Robert W. Leland, Darryl J. Melander, Ray W. Meyers, Scott A. Mitchell,
and Timothy J. Tautges,
The Geode Algorithm: Combining Hex/Tet Plastering,
Dicing and Transition Elements
for Automatic, All-Hex Mesh Generation,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 515-521, October 1998.
PostScript. Borlin Shyu.
Robert W. Leland, Darryl J. Melander, Ray W. Meyers, Scott A. Mitchell,
and Timothy J. Tautges,
The Geode Algorithm: Combining Hex/Tet Plastering,
Dicing and Transition Elements
for Automatic, All-Hex Mesh Generation,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 515-521, October 1998.
PostScript. Borlin Shyu.
An interesting real-world paper that gives you an idea what kinds of
clever tricks and compromises people make
when they write industrial meshing software.
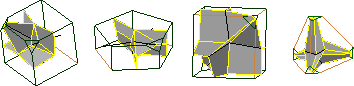 Alla Sheffer, Michal Etzion, Ari Rappoport, and Michel Bercovier,
Hexahedral Mesh Generation using the Embedded Voronoi Graph,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 347-364, October 1998.
PostScript.
Alla Sheffer, Michal Etzion, Ari Rappoport, and Michel Bercovier,
Hexahedral Mesh Generation using the Embedded Voronoi Graph,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 347-364, October 1998.
PostScript.
A polyhedral decomposition approach to hexahedral mesh generation.
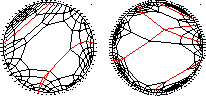 Timothy J. Tautges, Ted Blacker, and Scott Mitchell,
The Whisker Weaving Algorithm: A Connectivity-Based Method for Constructing
All-Hexahedral Finite Element Meshes.
PostScript.
You might also find it useful to consult the more detailed description
of the spatial twist continuum in
Peter Murdoch, Steven Benzley, Ted Blacker, and Scott A. Mitchell,
The Spatial Twist Continuum Captures the Global Connectivity of an
All-Hexahedral Finite Element Mesh
(PostScript).
Jason Riedy.
Timothy J. Tautges, Ted Blacker, and Scott Mitchell,
The Whisker Weaving Algorithm: A Connectivity-Based Method for Constructing
All-Hexahedral Finite Element Meshes.
PostScript.
You might also find it useful to consult the more detailed description
of the spatial twist continuum in
Peter Murdoch, Steven Benzley, Ted Blacker, and Scott A. Mitchell,
The Spatial Twist Continuum Captures the Global Connectivity of an
All-Hexahedral Finite Element Mesh
(PostScript).
Jason Riedy.
Whisker weaving is the most sophisticated approach to
unstructured hexahedral mesh generation of general shapes.
It's difficult to understand and implement,
but it's probably going to be the best once the theory is better sorted out.
Ask me for a companion paper that describes the Spatial Twist Continuum (STC)
in greater detail; it has some helpful figures.
(In fact, you might wind up mostly just presenting the STC paper.)
 Brian Curless and Marc Levoy,
A Volumetric Method for Building Complex Models from Range Images,
Computer Graphics (SIGGRAPH '96 Proceedings), pages 303-312, 1996.
Brian Curless and Marc Levoy,
A Volumetric Method for Building Complex Models from Range Images,
Computer Graphics (SIGGRAPH '96 Proceedings), pages 303-312, 1996.
One of the best-known methods for building surfaces to fit point data.
Unlike the method I'll teach in class, it has no guaranteed bounds,
but it works well in practice.
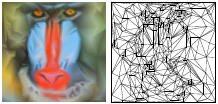 Michael Garland and Paul Heckbert,
Fast Triangular Approximation of Terrains and Height Fields,
manuscript, May 1997.
PostScript. Okan Arikan.
Michael Garland and Paul Heckbert,
Fast Triangular Approximation of Terrains and Height Fields,
manuscript, May 1997.
PostScript. Okan Arikan.
For applications in Geographical Information Systems and terrain databases,
it is useful to be able to simplify triangulated terrains
for coarse or fast rendering.
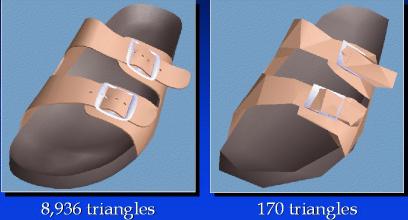
 Michael Garland and Paul Heckbert,
Surface Simplification Using Quadric Error Metrics,
Computer Graphics (SIGGRAPH '97 Proceedings), August 1997.
PostScript.
Slides from their
talk (PDF) are also available.
Andy Neureuther.
Michael Garland and Paul Heckbert,
Surface Simplification Using Quadric Error Metrics,
Computer Graphics (SIGGRAPH '97 Proceedings), August 1997.
PostScript.
Slides from their
talk (PDF) are also available.
Andy Neureuther.
Here, we are interested in simplifying general triangulated surfaces
embedded in three-dimensional space.
These surfaces may be much more complicated than terrains.
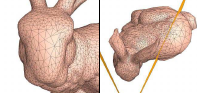 Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 189-198, August 1997.
PostScript.
Slides from Hugues'
talk (PDF) are also available.
Tolga Goktekin.
Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 189-198, August 1997.
PostScript.
Slides from Hugues'
talk (PDF) are also available.
Tolga Goktekin.
Progressively simplified triangular surfaces can be rendered at
different levels of detail,
depending on how they are viewed.
That way, you can trade off detail and rendering time.
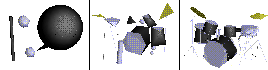 Jovan Popovic and Hugues Hoppe,
Progressive Simplicial Complexes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 217-224, August 1997.
PostScript.
Slides from Hugues'
talk (PDF) are also available.
Michael Downes.
Jovan Popovic and Hugues Hoppe,
Progressive Simplicial Complexes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 217-224, August 1997.
PostScript.
Slides from Hugues'
talk (PDF) are also available.
Michael Downes.
A simplification/compression method that preserves topological,
as well as geometric, information.
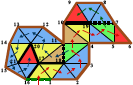 Jarek Rossignac,
Edgebreaker: Connectivity Compression for Triangle Meshes,
Technical Report GIT-GVU-98-35, GVU Center, Georgia Institute of Technology,
October 1998.
PostScript. Tzi-cker Chiueh.
Jarek Rossignac,
Edgebreaker: Connectivity Compression for Triangle Meshes,
Technical Report GIT-GVU-98-35, GVU Center, Georgia Institute of Technology,
October 1998.
PostScript. Tzi-cker Chiueh.
A discussion of methods for compression of triangular meshes for
rapid transmission over slow communication lines.