CS 184: COMPUTER GRAPHICS
PREVIOUS
< - - - - > CS
184 HOME < - - - - > CURRENT
< - - - - > NEXT
Lecture #14 -- Wed 3/11/2009.
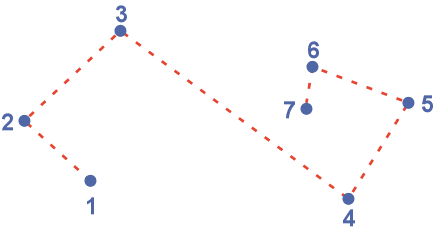
A) Approximate this curve with C1 continuity
using four cubic Bézier segments.
|
B) Create a G1-continuous, interpolating spline through all
numbered data points, using cubic Bézier segments.
|

|
|
Practical solution for A)
- Split the whole curve into 4 pieces that all have about the same amount of total absolute turning in them (better than splitting by arc-length!).
- Place the control points that correspond to the joined ends of two consecutive Bezier segments at these splitting points.
- Take the tangent directions at these points from the given curve.
- Place the inner control points for each Bezier segment
onto these tangent lines, at a distance that observes the convex hull property
and leads to eaqual velocities on both sides of the junction (some compromising may be necessary).
Practical solution for B)
- Put a Bezier segments between every pair of subsequent data points.
The given data points thus are the endpoints of the Bezier segments, and the subdivision of the curve is implicitly given.
- Now we need to choose good tangent directions at all the data points (that is where the inner Bezier control points will be placed).
- Heuristic 1 (based on Catmull-Rom spline): Make tangent
parallel to the chord between the two nearest neighbor data points.
- Heuristic 2: Make tangent perpendicular to the angle divider in the (red-dashed) connectivity polygon at this point.
- Now we need to pick a good distance from the data points for all the inner control points:
- Heuristic 1 (based on Catmull-Rom spline): 1/6 of chord length
between the two neighbor points (this gives actually C1
continuity).
- Heuristic
2: Place the control points individually 1/3 of the length of the
associated chord away from the data point (only G1 continuity).
Cubic Bezier Curves (continued)
Basic
underlying math;
Cubic Bezier Curve: 2 endpoints, 2 approximated intermediary control
points:
(P1,P2) = 1/3 of starting velocity vector; (P3,P4) = 1/3 of ending velocity vector
How many DOF's in a cubic Bezier segment in the plane ?
Properties of Bezier Curves
Cubic polynomial, ==> true space curves;
Interpolates endpoints;
Approximation of other two control points;
End tangents defined by pairs of control points;
Convex hull property; (curve lies completely inside the convex hull around its control polygon)
Variation diminishing property; (curve does not cross any straight line more often than its control polygon)
Invariant under affine transformations; (just need to transform the control points ...)
Start-to-end symmetry;
Infinitely differentiable;
May have loops, cusps.
Construction of Bezier Curves
DeCasteljau
construction algorithm: (Construction by three iterations of linear
interpolation)
The role of the control points.
-- How to draw a Bezier curve from its control points:
-- Subdivision of a Bezier curve into two pieces
that together are identical to the original one.
How
to put two Bezier segments together with G1 or with C1 continuity.
B-Spline Curves
An easy way to make a smooth C2-continuous space curve for a path of an
airplane or for a camera path is to sprinkle a few control points through
space that define the coarse topology and geometry of the curve and then
let them be approximated by a
cubic B-spline.
In a nutshell, one segment depending on the 4 control points A,B,C,D,
is given by the polynomial:
Q = A(1 -3t +3t2 -t3)/6 + B(4 -6t2 +3t3)/6 + C(1
+3t +3t2 -3t3)/6 + D(t3)/6
thus the point at t=0 is given by A/6 + 4B/6 + C/6,
and the point at t=1 is given by B/6 + 4C/6 + D/6.
Assuming for the moment a closed curve with N=6 control
points, such a curve would be described as a sequence
of N=6 cubic curve segments, each one of which is controlled by four
consecutive control points, but producing a curve segment that is only
about as long as the distance between the two middle control points. Because
a subsequent curve segment reuses three of the control points of the previous
segment, they blend together in a very smooth (C2-continuous) way.
[More on that in CS284]
Properties of Cubic B-Splines
Piecewise cubic polynomial;
Does
NOT interpolate control points;
Convex hull property;
Construction by 3-fold linear interpolation; (similar to the one for Bezier curves)
Invariant under affine transformations;
Start-to-end symmetry;
Twice differentiable (C2) at joints;
Infinitely differentiable everywhere else;
May have cusps, thus may not be G2 everywhere;
Good to make smooth
closed loops.
Reading Assignments:
Skim:
Shirley, 2nd Ed: Ch 15
Study: ( i.e., try to understand fully, so that you can answer
questions
on an exam):
Shirley, 2nd Ed: Ch 15.6-15.7
Take-Home-Exam: from Monday 3/9 till Wednesday 3/11 start of class.
Programming Assignment 6: due (electronically submitted) before Tuesday 3/17, 11pm <== THIS ASSIGNMENT CAN BE DONE IN PAIRS !
ADVICE: Start this assignment TODAY!
It is not a good approach to "power through" any of these assignments
in a single session. There will always be points where you will get
stuck in your programming and just cannot find some silly little
mistake for many hours. It is good to be able to walk away from
your computer and come back the next day -- and then find that mistake
often within minutes. Also, the earlier you start, the sooner you
know what the issues are that may give you problems, and the more
opportunities you have to ask someone for clarification.
PREVIOUS
< - - - - > CS
184 HOME < - - - - > CURRENT
< - - - - > NEXT