CS 184: COMPUTER GRAPHICS
PREVIOUS
< - - - - > CS
184 HOME < - - - - > CURRENT
< - - - - > NEXT
Lecture #19 -- Mon 4/6/2009.
|
 |
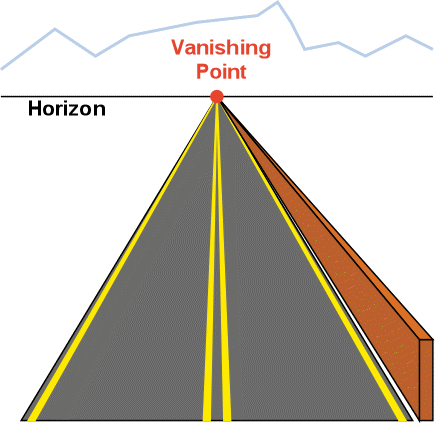
How (by what geometrical construction)
can you find the exact location in the
image plane of the vanishing point of
a given set of parallel lines or edges ?
|
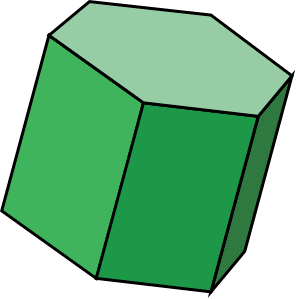
What is the maximal / minimal number of vanishing points that
can result from a perspective projection onto the image plane of the
above hexagonal prism (depending on its orientation with respect to the
imaging plane) ?
|
PREPARATION FOR MIDTERM (Wednesday !)
Prepare your one sheet of notes.
Get a good night's sleep before the exam.
Rules for the exam:
Clean desks: just your writing utensils, the exam, the help sheet; no calculators or other electronic devices.
Quiet room: no distractions, ask no questions, don't leave the room.
The Classical Rendering Pipeline (cont.)
There are many different camera types and projection situations ...
How do you conveniently and unambiguously specify all required camera/viewing
parameters ?
- Position and orient the camera with the "look_at" transformation. (This defines the geometry of the VRCS completely).
- The z-axis (n-axis) is the view plane normal.
- A rectangle in the viewing plane (z = -1) specifies the size of the film (and thus the lateral dimensions of the viewing
volume).
- If the center of that rectangle lies on the -z-axis (-n-axis), we get a
symmetrical view volume (else we get a somewhat slanted view).
- A slanted view in parallel projection allows us to do oblique projections.
This will require a shear transformation to get
such a view volume into the canonical viewing box. - Two z-values specify back and front cutoff planes and thereby define a finite 3D volume of interest.
These will get normalized to the back and front faces of the canonical brick-like viewing box.
How does the final image change, as we change some of the parameters of the perspective projection ?
In the perspective case, the size of the image depends on the
distance
between camera and original.
The key feature is that geometry further away gets reduced by the factor 1/distance.
Rather than doing a real projection -- and thereby loosing the depth (ordering)
information,
we perform a 3D
to 3D transformation of the piece of the World that we are interested in
into a canonical view volume where it is easy to do culling
and clipping.
- First we perform a shear operation (if necessary) to bring the center
of the window n the n=-1 plane
(which specifies the opening of the view frustum)
onto the n-axis.
- Then we perform a non-uniform scaling in all three axes so that the
half-angles of the view frustum
in the x- and y-directions are set at 45 degrees, and so that the back
clipping plane is brought to n=-1.
- This is all very similar to the case of parallel projection; but now
comes the really nifty step:
The
Perspective Transformation:
This is a clever 3D to 3D transformation (using homogeneous coordinates)
that distorts the u and v dimensions in just the right way,
so as to achieve
a proper perspective look, when we finally perform a parallel projection along the n-axis.
It also maintains all relative orderings in the n-direction, so that
we can do hidden surface elimination later.
Furthermore, it keeps the back clipping plane (B) at the n=-1 plane,
and it moves the front clipping plane (F) to the n=0 plane.
[ Shirley takes an intermediate step and keeps (B) and (F) in the same place; this yields a simpler "perspective matrix" Mp ]
Now we have the whole view volume mapped into the same canonical half-brick as in the case of a parallel projection.
In general, it maps the point {x, y, z, 1} into {x, y, (z - zmin)/(1
+ zmin), -z}
.
It also maps the eye to infinity.
Furthermore, rays through the eye become parallel;
and parallel lines converge in a point called the Vanishing Point.
The Actual Projection to 2D
Once we have everything of interest within the canonical half-cube, doing the projection to 2D is trivial:
Just set the z-coordinate to zero !
How do the coordinates coming from an original object get changed during
the projection step ?
Rather than just carying out projections, we do a full 3D->3D transformation
that produces the same effect on the x- and y- coordinate values
but also preserves the relative ordering of the geometry in the z-direction.
NOTE: Different books use different formalisms and even different canonical viewing volumes.
In 1996 Jim Blinn suggested to use a full (double) unit cube for the canonical viewing volume (twice the half-brick used above).
Some of the textbooks followed his advice and some didn't.
Shirley does use the full canonical cube going from +1 to -1 in z.
The math for that case is very well described in Chapter 7. Read it carefully.
In particular, Shirley, derives a simple perspective matrix, Mp,
that takes a symmetrical view frustum and orthogonalizes it into
a "brick" with the same front face and the same back plane but shrunk
back face; this brick is subsequently mapped to the canonical (full)
brick.
It can just as easily be mapped into the traditional half-brick using the same perspective matrix.
The key concepts are exactly the same in both cases, but the resulting perspective transformation matrix is somewhat different.
You can find the gory detailed math for the canonical half-brick version here:
Camera
Specifications and Mapping of the Viewing Volume into the Canonical Half-Cube.
MIDTERM MATERIAL ENDS HERE
Polygon Clipping in 3D
Polygons (triangles) are the basic primitives that we are rendering.
We need to clip them around the (display) window edges, so that we don't
send invalid addresses to the display bit-planes.
But we also want to clip against an additional front- and back-clipping plane, so that we can cull away a lot of visual clutter in the scene.
But there are some new potential problems that make clipping really
essential (and we can't even defer it to the very end, and just do it in 2D !)
Perspective
images of line segments
Study the various cases where the endpoints of a line segment may lie:
1.) Both in front of the eye: ==> OK
2.) Both behind the eye: ==> No problem; but do we want to see this
?
3.) One in front, one behind: ==> Problems! Image goes through infinity!
Clipping is crucial.
On the other hand you can see the point at infinity of the original
line: This is the "Vanishing Point"
Various Clipping Options
1.) Do it in z first, to avoid above wrap-around problem, and then do more
clipping later in 2D;
This is conceptually plausible, but inelegant, since
it involves two different clipping steps.
2.) Do it in 3D on the canonical view frustum;
This is doable, but it involves more complex expressions for the sides of the frustum.
3.) Do
it in 4D in the space of the homogeneous coordinates;
This is the most elegant solution, and it has very simple numerical values.
Reading Assignments:
Study:
Shirley, 2nd Ed: Ch 7; and again Ch 12.
Programming Assignment 8: due (electronically submitted) before Saturday 4/11, 11pm
In-class Mid-term-Exam: WED 4/8, 2:40-4:00pm
PREVIOUS
< - - - - > CS
184 HOME < - - - - > CURRENT
< - - - - > NEXT
Page Editor: Carlo
H. Séquin