Inverse Kinematics, Formal Approach

PREVIOUS < - - - - > CS 184 HOME < - - - - > CURRENT < - - - - > NEXT

Finding the Jacobian and its Inverse:

Given the function: E = f(q), where E is of dimension n (e.g., the number of constraints), and q is of dimension m (e.g., the DoF of the linkage), the Jacobian J is then the n by m matrix of partial derivatives, where the (i,j)th element of J is given by: J_ij =df_i /dq_jIt computes differential changes in E, expressed as dE, in terms of differential changes of q, expressed as dq :

dE = J(q) dq.

The Jacobian can be calculated in closed form, if the function f is simple enough.
In more difficult cases we can use finite differencing:

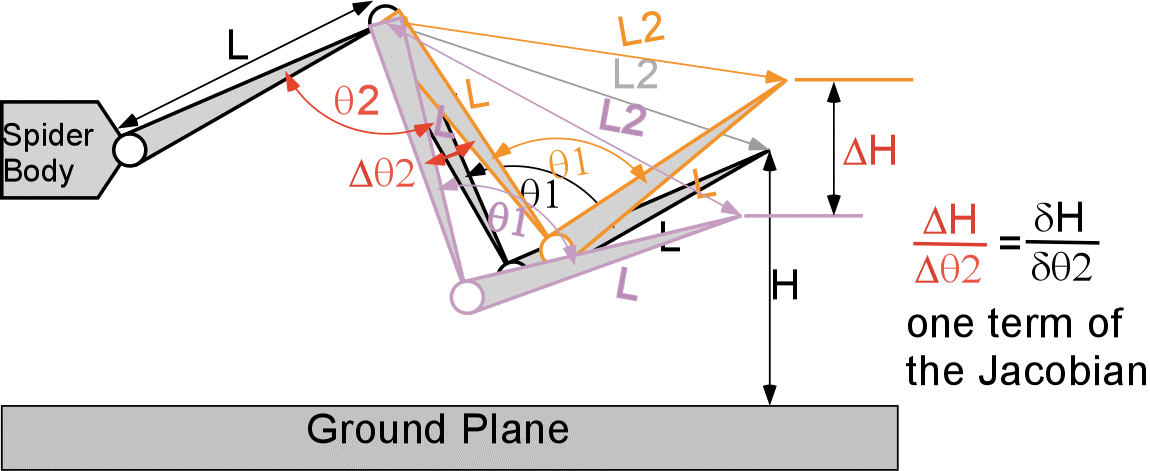
In this manner we can construct a Jacobian for any system!
Now we "just need to invert" the equation above, and then take small steps from the current state: dq= J^-1(dE).
dq is the vector of the (small) changes that need to be made to the state vector to reduce the error by dE.
After every step the Jacobian needs to be recomputed.

But the Jacobian itself may not invertible (e.g., if it is not square). The problem may be over- or under-constrained.

Thus we construct a pseudo-inverse:
Using SVD: J = Q S P^T where S is a (possibly non-square) diagonal matrix.
For this we can find the inverse as: J^-1 = P S^-1 Q^T-- but some diagonal values = 0 ! ==> Just set 1/0 to 0.0

For more details, study:
Numerical Methods for Inverse Kinematics, by Niels Joubert, UC Berkeley, written for CS184.

Using the Jacobian Transpose instead:

Rather than using the pseudo-inverse of the Jacobian, we can use its transpose: dq= J^T(dE).
This avoids the expensive process of SVD and matrix inversion.
It is a plausible, justifyable approach, because it is related to the method of steepest decent.
( It follows a force that pulls the end-effector towards its desired target location).

And here is an even more direct, "greedy" approach: CCD:

Cyclic Coordinate Descent:

We break the overall IK problem into a series of 1-DoF IK problem that we solve by iterating cyclically through all the variables.
These simple 1-Dof Ik problems have analytical solutions:
For each we adjust the value under consideration, so as to minimize the error function (e.g., distance from target).
This method does take more iteration steps and it does not always lead to a smooth approach to the target.
But we can "damp" CCD to make it smooth -- instead of moving each joint to the exact optimal, we only move it partway there in each step.
(Depending on step size, the Jacobian methods may also be unsmooth!)

For more details, study:
Presentation by Bill Baxter, UNC.