CS 39R: Symmetry & Topology
Lecture #8 -- Mon. 4/1, 2013.
PREVIOUS <- - - - > CS 39R HOME < - - - - > CURRENT < - - - - > NEXT
Preparation:
Design a Highway 'Cloverleaf' for a Crossing of Three
Highways.
Think about ways in which to evaluate your design with respect
to the trade-off between efficiency and costs.
Warm-up:
Some objective measures are needed to judge the
quality and efficiency of a design as well as its
realization costs:
In your design, how many extra "connecting arcs" did
you add? -- how many bridges?
In the worst case, through how many connecting
arcs/bridges does a car have to travel to find the
desired direction?
Discuss your cloverleaf layout and
your design parameters with your neighbors!
Highway Cloverleaf Design
Engineering Design typically has one or more clearly stated
goals, often with different priorities. Make sure you identify
these goals and keep track of them throughout the whole Design
process!
Engineering projects also have constraints and limitations:
budget; weight; space needed; material
strength . . . But some constraints are often more
flexible than others (e.g., budget vs. gravity).
Some diagrams to
back-up our in-class discussions.
Crossing-free graph-embeddings on a
2-manifold of suitable genus lies right at the heart of
topology!
Follow-up: On the Embedding of the Complete Graph K8 in a
genus-2 surface:
The math literature says that it is doable! (- even though
the references I found don't actually give the solution).
If you choose to work on this puzzle over the Spring break, keep
track of the various approaches that you are pursuing, and which
one of them look more promising.
Discussion of some more or
less promising approaches . . .
Diagrams
of my own struggles with this non-trivial graph-embedding
problem.
Wrap-up: Simple
topological 2-manifolds, -- orientable and
non-orientable
Last time we discussed: PPT
presentation.
Classification of 2-Manifolds
Each closed surface can be constructed from an oriented
polygon with an even number of sides,
called a fundamental polygon of the
surface, by pairwise identification of its edges.
Restricting ourselves to rectangles, in square below,
attaching the sides with matching labels (A with A,
B with B),
so that the arrows point in the same direction, yields the
indicated surface (as detailed in the PPT presentation above):
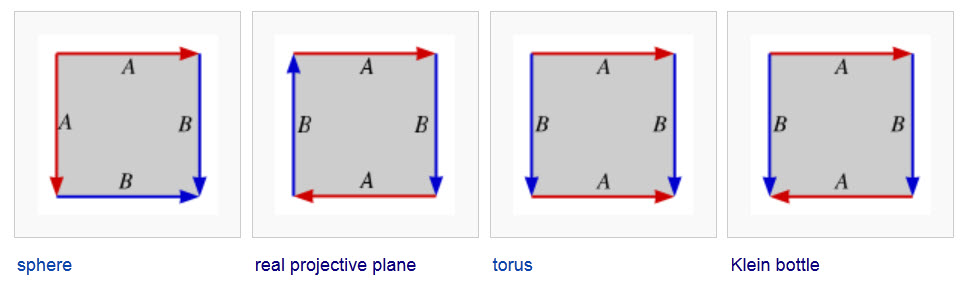
Classification Theorem of Closed Surfaces:
Any connected, closed (h=0, no
punctures) surface is "homeomorphic" to some member of one of
the following three families:
The SPHERE: 2-sided, X=2;
A connected sum of g TORI, (for g
>= 1) -> "Handles on a sphere": 2-sided,
genus=g, X= 2 - 2g;
A connected sum of k PROJECTIVE
PLANES, (for k >= 1) -> "Cross-caps on a
sphere": Single-sided, genus=k, X= 2-k.
Surfaces with Holes and Boundaries
If we allow surfaces to have "punctures" or "holes" --
which then have "boundaries" or "rims"
-- things get a little more complicated.
But a topologist can still classify all the possible surfaces of
that kind by only three characteristics:
ORIENTABILITY: Is the surface two-side (orientable)
or single-sided (non-orientable)?
# OF BOUNDARY COMPONENTS: How many "disks" have been
removed from a closed surface;
or, how many individual rims or hole contours, h, are there?
EULER CHARACTERISTIC, X (or alternatively, its GENUS,
g): How "connected" is the surface?
X = #Vertices - #Edges + #Facets of a mesh
approximating the surface.
Regular Homotopies (a more specific
classification)
Which surfaces are transformable into one another through
a "Regular Homotopy",
i.e., a deformation that allows surface regions to pass through
one another,
but does not allow any cuts, or tears, or formation of creases
or other singular points with infinite curvature.
(With this definition, it is possible to turn a sphere or a
torus inside out -- but it is not easy!).
Next class will begin with some preparatory
exercises:
-- Simplify the double 8 curve . . .
-- Try to turn a circle inside-out . . .
In preparation for that class, look at some of these movies:
Torus
eversion by Cheritat (cut open,
to see inside);
Turning
a sphere inside out by Max;
Turning
a sphere outside in by Thurston (more details
Levy,
Maxwell, Munzner);
Energetically
optimal sphere eversion by Sullivan, Francis, Levy.
New Homework Assignments: Due April 8,
2013, before noon:
Give me a brief update on your projects: One
paragraph summarizing your findings so far.
Please sen me e-mail before noon on Monday.
PREVIOUS <- - - - > CS 39R HOME < - - - - > CURRENT < - - - - > NEXT
Page Editor: Carlo H. Séquin
